Det finns föremål som kan ändra tätheten av det elektromagnetiska strålningsflödet som faller på dem, det vill säga antingen öka det genom att samla det vid en punkt eller minska det genom att sprida det. Dessa föremål kallas linser i fysiken. Låt oss titta närmare på det här problemet.
Vad är linser i fysik?
Detta koncept betyder absolut alla föremål som kan ändra utbredningsriktningen för elektromagnetisk strålning. Detta är den allmänna definitionen av linser i fysik, som inkluderar optiska glasögon, magnetiska och gravitationslinser.
I den här artikeln kommer fokus att ligga på optiska glasögon, som är föremål gjorda av ett transparent material och begränsat av två ytor. En av dessa ytor måste nödvändigtvis ha krökning (det vill säga vara en del av en sfär med ändlig radie), annars kommer objektet inte att ha egenskapen att ändra utbredningsriktningen för ljusstrålar.
Linsens princip

Kärnan i arbetet med detta okompliceradeoptiskt objekt är fenomenet brytning av solens strålar. I början av 1600-talet publicerade den berömde holländska fysikern och astronomen Willebrord Snell van Rooyen brytningslagen, som för närvarande bär hans efternamn. Formuleringen av denna lag är som följer: när solljus passerar genom gränsytan mellan två optiskt transparenta medier, då produkten av sinusen av infallsvinkeln mellan strålen och normalen till ytan och brytningsindexet för mediet där det sprider sig är ett konstant värde.

För att förtydliga ovanstående, låt oss ge ett exempel: låt ljuset falla på vattenytan, medan vinkeln mellan normalen till ytan och strålen är θ1. Sedan bryts ljusstrålen och börjar sin utbredning i vattnet redan i en vinkel θ2 mot normalen mot ytan. Enligt Snells lag får vi: sin(θ1)n1=sin(θ2) n2, där n1 och n2 är brytningsindex för luft och vatten, respektive. Vad är brytningsindex? Detta är ett värde som visar hur många gånger utbredningshastigheten för elektromagnetiska vågor i vakuum är högre än för ett optiskt transparent medium, det vill säga n=c/v, där c och v är ljusets hastigheter i vakuum och i medium, respektive.
Fysiken för uppkomsten av brytning ligger i implementeringen av Fermats princip, enligt vilken ljus rör sig på ett sådant sätt att det övervinner avståndet från en punkt till en annan i rymden på kortast tid.
Typer av linser

Typen av optisk lins i fysiken bestäms enbart av formen på ytorna som bildar den. Brytningsriktningen för strålen som infaller på dem beror på denna form. Så om ytans krökning är positiv (konvex), kommer ljusstrålen, när den lämnar linsen, att fortplanta sig närmare sin optiska axel (se nedan). Omvänt, om krökningen av ytan är negativ (konkav), och sedan passerar genom det optiska glaset, kommer strålen att röra sig bort från sin centrala axel.
Observera igen att en yta med valfri krökning bryter strålar på samma sätt (enligt Stellas lag), men normalerna till dem har en annan lutning i förhållande till den optiska axeln, vilket resulterar i ett annat beteende hos den brutna strålen.
En lins som begränsas av två konvexa ytor kallas en konvergerande lins. I sin tur, om det bildas av två ytor med negativ krökning, kallas det spridning. Alla andra typer av optiska glasögon är förknippade med en kombination av dessa ytor, till vilka ett plan också läggs till. Vilken egenskap den kombinerade linsen kommer att ha (divergent eller konvergerande) beror på den totala krökningen av radierna på dess ytor.
Linselement och strålegenskaper

För att bygga in linser i bildfysik måste du bekanta dig med elementen i detta objekt. De är listade nedan:
- Optisk huvudaxel och centrum. I det första fallet betyder de en rak linje som går vinkelrätt mot linsen genom dess optiska centrum. Den senare är i sin tur en punkt inuti linsen som passerar genom vilken strålen inte upplever brytning.
- Brännvidd och fokus - avståndet mellan mitten och en punkt på den optiska axeln, som samlar alla strålar som faller in på linsen parallellt med denna axel. Denna definition gäller för insamling av optiska glasögon. När det gäller divergerande linser är det inte själva strålarna som kommer att konvergera till en punkt, utan deras imaginära fortsättning. Denna punkt kallas huvudfokus.
- Optisk kraft. Detta är namnet på den ömsesidiga brännvidden, det vill säga D \u003d 1 / f. Det mäts i dioptrier (dioptrier), det vill säga 1 dioptri.=1 m-1.
Följande är huvudegenskaperna hos strålarna som passerar genom linsen:
- strålen som passerar genom det optiska centrumet ändrar inte dess rörelseriktning;
- strålar som faller in parallellt med den optiska huvudaxeln ändrar sin riktning så att de passerar genom huvudfokuset;
- strålar som faller på optiskt glas i valfri vinkel, men passerar genom dess fokus, ändrar sin utbredningsriktning på ett sådant sätt att de blir parallella med den optiska huvudaxeln.
Ovanstående egenskaper hos strålar för tunna linser i fysik (som de kallas eftersom oavsett vilka sfärer de bildas och hur tjocka de är, bara objektets optiska egenskaper) används för att bygga bilder i dem.
Bilder i optiska glasögon: hur bygger man?
Nedan är en figur som beskriver scheman för att konstruera bilder i de konvexa och konkava linserna på ett objekt(röd pil) beroende på dess position.
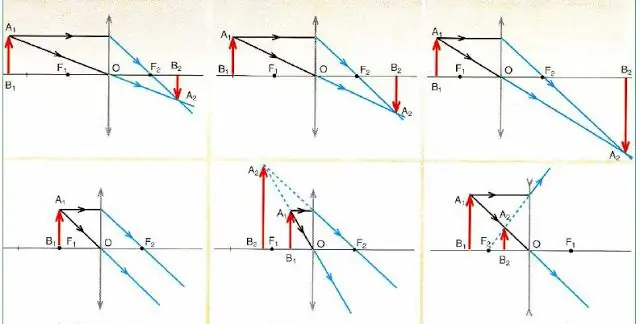
Viktiga slutsatser följer av analysen av kretsarna i figuren:
- Vilken bild som helst bygger på endast 2 strålar (passerar genom mitten och parallellt med den optiska huvudaxeln).
- Konvergerande linser (markerade med pilar i ändarna som pekar utåt) kan ge både en förstorad och förminskad bild, som i sin tur kan vara verklig (riktig) eller imaginär.
- Om objektet är i fokus, bildar inte linsen sin bild (se det nedre diagrammet till vänster i figuren).
- Spridande optiska glasögon (markerade med pilar i ändarna som pekar inåt) ger alltid en förminskad och virtuell bild oavsett objektets position.
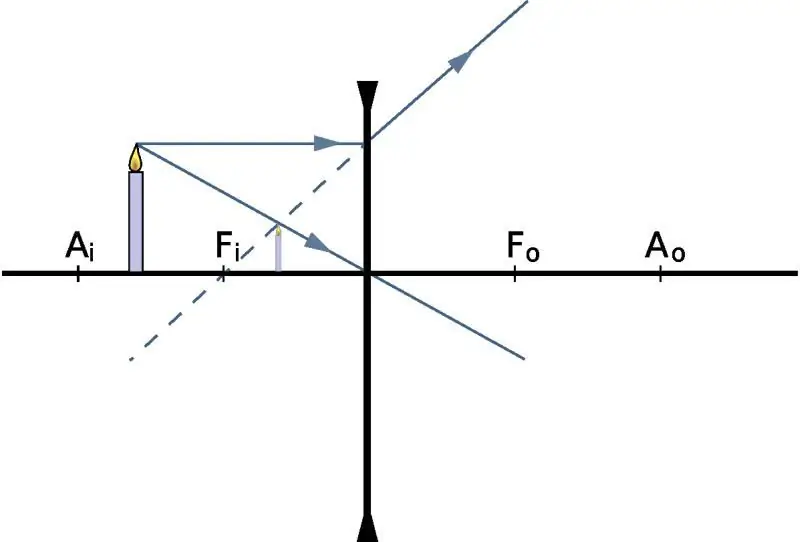
Hitta avståndet till en bild
För att bestämma på vilket avstånd bilden kommer att visas, med kunskap om själva objektets position, ger vi linsformeln i fysik: 1/f=1/do + 1 /d i, där do och di är avståndet till objektet och dess bild från optiken centrum, respektive, f är huvudfokus. Om vi pratar om ett samlande optiskt glas, kommer f-numret att vara positivt. Omvänt, för en divergerande lins är f negativ.
Låt oss använda den här formeln och lösa ett enkelt problem: låt objektet vara på ett avstånd do=2f från mitten av det optiska glaset. Var kommer hans bild att synas?
Från problemets tillstånd har vi: 1/f=1/(2f)+1/di. Från: 1/di=1/f - 1/(2f)=1/(2f), dvs. di=2 f. Bilden kommer alltså att visas på ett avstånd av två brännpunkter från linsen, men på andra sidan än själva objektet (detta indikeras av det positiva tecknet för värdet di).
En kort historik
Det är intressant att ge ordet "lins" etymologin. Det kommer från de latinska orden lens och lentis, som betyder "lins", eftersom optiska föremål i sin form verkligen ser ut som frukten av denna växt.
Bröjningskraften hos sfäriska genomskinliga kroppar var känd för de gamla romarna. För detta ändamål använde de runda glaskärl fyllda med vatten. Själva glaslinser började tillverkas först på 1200-talet i Europa. De användes som ett läsverktyg (moderna glasögon eller ett förstoringsglas).
Den aktiva användningen av optiska objekt vid tillverkning av teleskop och mikroskop går tillbaka till 1600-talet (i början av detta århundrade uppfann Galileo det första teleskopet). Observera att den matematiska formuleringen av Stellas brytningslag, utan kunskap om vilken det är omöjligt att tillverka linser med önskade egenskaper, publicerades av en holländsk vetenskapsman i början av samma 1600-tal.
Andra linser
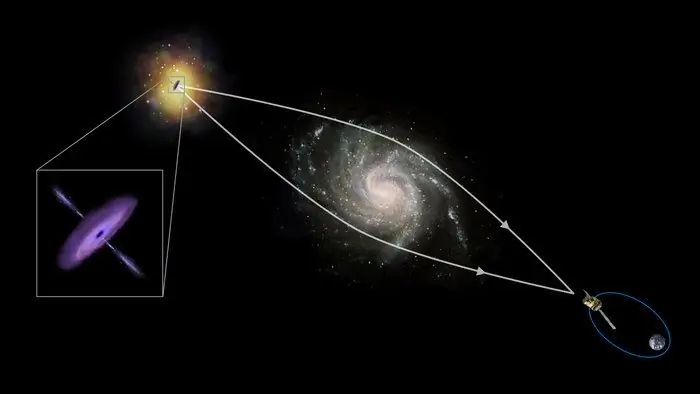
Som nämnts ovan finns det förutom optiska brytningsobjekt även magnetiska och gravitationsobjekt. Ett exempel på de förra är magnetiska linser i ett elektronmikroskop, ett levande exempel på det senare är förvrängningen av ljusflödets riktning,när den passerar nära massiva rymdkroppar (stjärnor, planeter).






