När expertgranskning, till exempel, bedömer produkters konkurrenskraft, är det nödvändigt, som i alla vetenskapliga arbeten, att utföra statistisk databehandling. Det senare börjar med att bestämma överensstämmelsen i expertutlåtanden, vars numeriska uttryck är konkordanskoefficienten.
Varför behöver vi en expertbedömning?
Denna bedömning är nödvändig, först och främst, eftersom experternas åsikter kan skilja sig mycket åt vad gäller de uppskattade parametrarna. Inledningsvis görs bedömningen genom att rangordna indikatorerna och tilldela dem en viss betydelsekoefficient (vikt). En inkonsekvent rangordning resulterar i att dessa koefficienter är statistiskt opålitliga. Yttrandena från experter med det antal som krävs (fler än 7-10) bör distribueras enligt normal lag.
Begreppet konkordanskoefficient
Så. Konsekvens är konkordans. Koefficienten är en dimensionslös kvantitet som visar förhållandet mellan dispersionen och den maximala dispersionen i det allmänna fallet. Låt oss generalisera dessa begrepp.
Konkordanskoefficient är ett tal från 0 till 1, som visar konsekvensen i expertutlåtanden närrangordna vissa fastigheter. Ju närmare detta värde är 0, desto lägre anses konsistensen. Om värdet på denna koefficient är mindre än 0,3 anses experternas åsikter vara inkonsekventa. När värdet på koefficienten ligger i intervallet från 0,3 till 0,7 anses konsistensen vara genomsnittlig. Ett värde större än 0,7 anses vara hög konsistens.
Användningsfall
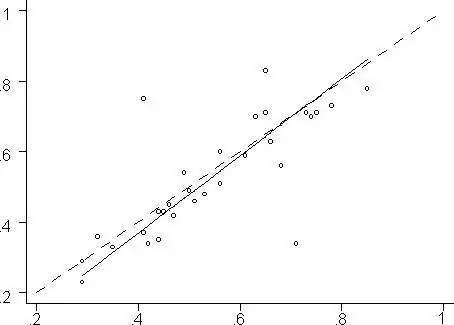
När man utför statistisk forskning kan det uppstå situationer där ett objekt inte kan karakteriseras av två sekvenser, som bearbetas statistiskt med hjälp av konkordanskoefficienten, utan av flera sekvenser, som följaktligen rangordnas av experter med samma nivå av professionalism inom ett visst område.
Konsistensen i den rangordning som utförs av experter måste bestämmas för att bekräfta riktigheten av hypotesen att experter gör relativt exakta mätningar, vilket möjliggör bildandet av olika grupperingar i expertgrupper, som till stor del bestäms av mänskliga faktorer, främst såsom skillnader i åsikter, begrepp, olika vetenskapliga skolor, arten av yrkesverksamhet etc.
Kort beskrivning av rangmetoden. Dess fördelar och nackdelar
Vid rankning används rankmetoden. Dess essens ligger i det faktum att varje egenskap hos objektet tilldelas sin egen specifika rang. Dessutom tilldelas varje expert som ingår i expertgruppen denna rangoberoende, vilket resulterar i ett behov av att bearbeta dessa uppgifter för att identifiera konsekvensen i expertutlåtanden. Denna process utförs genom att beräkna konkordanskoefficienten.
Den största fördelen med rankmetoden är dess enkla implementering.
De största nackdelarna med metoden är:
- ett litet antal rankningsobjekt, eftersom när deras antal överstiger 15-20 blir det svårt att tilldela objektiva rankingpoäng;
- Baserat på användningen av denna metod förblir frågan om hur långt de studerade objekten är från varandra i betydelse öppen.
När man använder den här metoden måste man ta hänsyn till att betygen är baserade på någon sorts sannolikhetsmodell, så de måste tillämpas med försiktighet med tanke på omfattningen.
Kendall's Concordance Rank Coefficient
Används för att bestämma förhållandet mellan kvantitativa och kvalitativa egenskaper som kännetecknar homogena objekt och rangordnas enligt samma princip.
Denna koefficient bestäms av formeln:
t=2S/(n(n-1)), där
S - summan av skillnaderna mellan antalet sekvenser och antalet inversioner på den andra egenskapen;
n - antal observationer.

Beräkningsalgoritm:
- X-värdena rangordnas i stigande eller fallande ordning.
- Y-värdena är ordnade i den ordning som de motsvarar x-värdena.
- För varje på varandra följande rankning av y, bestäm hur många högre rankningsvärden som följer den. De läggs ihop och måttet på överensstämmelse mellan sekvenser av rangordningar i x och y beräknas.
- På liknande sätt beräknas antalet y-grader med lägre värden, vilket också summerar.
- Lägg till antalet rankningar med högre värden och antalet ranks med lägre värden, vilket resulterar i värdet S.
Denna koefficient visar sambandet mellan två variabler och kallas i de flesta fall Kendalls rangkorrelationskoefficient. Sådant beroende kan representeras grafiskt.
Bestämning av koefficient
Hur går det till? Om antalet rankade egenskaper eller faktorer överstiger 2 används konkordanskoefficienten, som i huvudsak är en multipel variant av rangkorrelation.
Var försiktig. Beräkningen av konkordanskoefficienten är baserad på förhållandet mellan avvikelsen av summan av kvadrater av rang från medelsumman av kvadrater av rang, multiplicerat med 12, till kvadraten av experter, multiplicerat med skillnaden mellan kuben av talet av objekt och antalet objekt.
Beräkningsalgoritm
För att förstå var talet 12 kommer ifrån i täljaren i beräkningsformeln, låt oss titta på bestämningsalgoritmen.
För varje rad med en viss experts rankning beräknas summan av rankningarna, vilket är ett slumpmässigt värde.
Konkordanskoefficienten definieras generellt som förhållandet mellan variansuppskattningen (D) och det maximala värdet för variansuppskattningen(Dmax). Låt oss successivt formulera definitionerna av dessa kvantiteter.
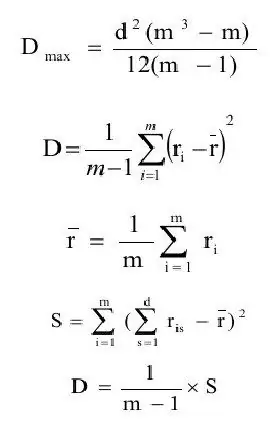
där ravg - förväntningsuppskattning;
m - antal objekt.
Genom att ersätta de resulterande formlerna i förhållande till D med Dmax får vi den slutliga formeln för konkordanskoefficienten:
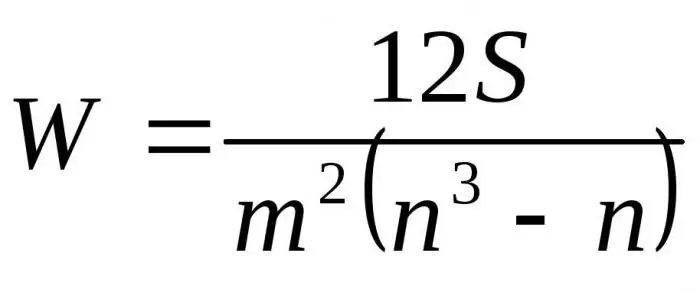
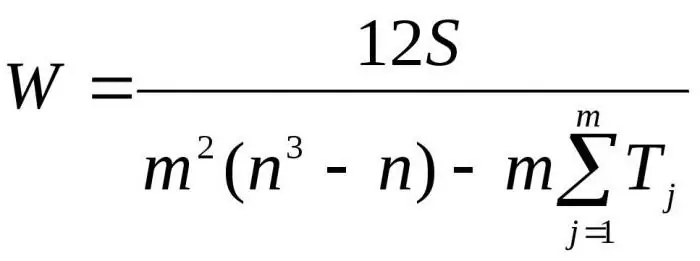
Här är m antalet experter, n är antalet objekt.
Den första formeln används för att bestämma konkordansfaktorn om det inte finns några relaterade rangordningar. Den andra formeln används om det finns relaterade ranger.
Så, beräkningen av konkordanskoefficienten är över. Vad kommer härnäst? Det erhållna värdet utvärderas för signifikans med hjälp av Pearson-koefficienten genom att multiplicera denna koefficient med antalet experter och med antalet frihetsgrader (m-1). Det resulterande kriteriet jämförs med tabellvärdet, och om värdet på det första överstiger det sista talar de om betydelsen av koefficienten som studeras.
När det gäller relaterade ranger blir beräkningen av Pearson-kriteriet något mer komplicerad och utförs med följande förhållande: (12S)/(d(m2+ m)-(1/(m-1))x(Ts1 +Ts2 +Tsn)
Exempel
Anta att expertmetoden utvärderar konkurrenskraften hos smör som säljs i ett detaljhandelsnätverk. Låt oss ge ett exempel på beräkning av konkordanskoefficienten. Innan man bedömer konkurrenskraften är det nödvändigt att rangordna konsumentenegenskaper hos denna produkt som är involverade i utvärderingen. Låt oss anta att dessa egenskaper kommer att vara följande: smak och lukt, konsistens och utseende, färg, förpackning och märkning, fetth alt, handelsnamn, tillverkare, pris.
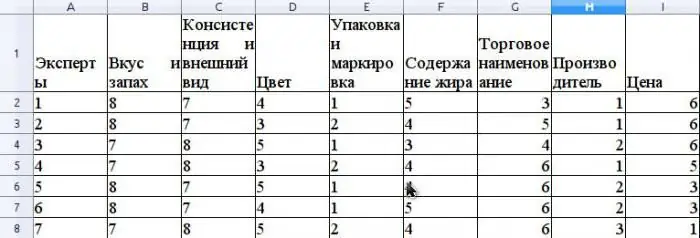
Anta att expertgruppen består av 7 experter. Figuren visar resultaten av att rangordna dessa egenskaper.
Medelvärdet för r beräknas som det aritmetiska medelvärdet och blir 31,5. För att hitta S, summera de kvadratiska skillnaderna mellan ris och r medelvärde, enligt formeln ovan och bestäm att värdet på S är 1718.
Beräkna konkordanskoefficienten med hjälp av formeln utan att använda relaterade rankningar (rankningar skulle vara relaterade om samma expertrådgivare hade samma rankning för olika egenskaper).
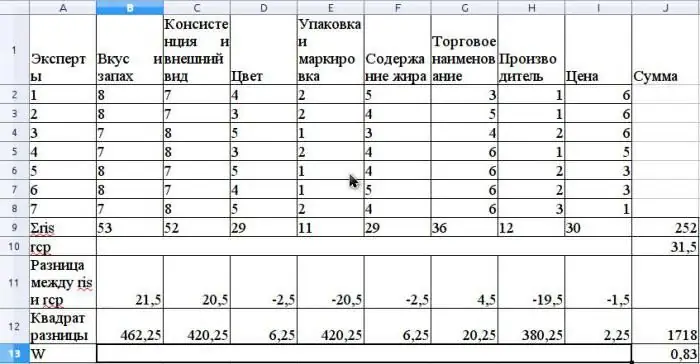
Värdet på denna koefficient kommer att vara 0,83. Detta indikerar en stark konsensus bland experter.
Kontrollera dess betydelse med Pearson-testet:
7 x 0,83 x (8-1)=40,7.
Pearsons tabelltest vid 1 % signifikansnivå är 18,5 och vid 5 % - 14,1..
Exemplet visar enkelheten och tillgängligheten i beräkningen för alla som kan grunderna i matematiska beräkningar. För att lindra dem,använd kalkylbladsformulär.
Avslutningsvis
Således visar överensstämmelsekoefficienten att flera experters åsikter är konsekventa. Ju längre det är från 0 och närmare 1, desto mer konsekventa åsikter. Dessa koefficienter måste bekräftas genom att beräkna Pearson-kriteriet.






