Propositionalgebra är en exakt vetenskap som inte kompromissar. För att lösa exempel med konjunktion, disjunktion, implikation och så vidare kan du bygga en sanningstabell i Excel-applikationen. Den är utrustad med en uppsättning logiska funktioner som automatiserar och underlättar processen att hitta resultatet.
Matematisk logik: grundläggande begrepp
Aristoteles anses vara grundaren av formell logik. På 1600-talet G. Leibniz föreslog att man skulle introducera symboler för att definiera påståenden. D. Buhl befäste den förvärvade kunskapen och markerade för första gången meningar med symboler.
Schematiskt ersätts "TRUE" med 1 och "FALSE" med 0.
Under uttalandet förstås varje deklarativ mening som ger all information och som kan ta värdet av sanning eller falskhet. I algebra abstraheras logik från den semantiska belastningen av meningar och tar endast hänsyn till logiska värden.
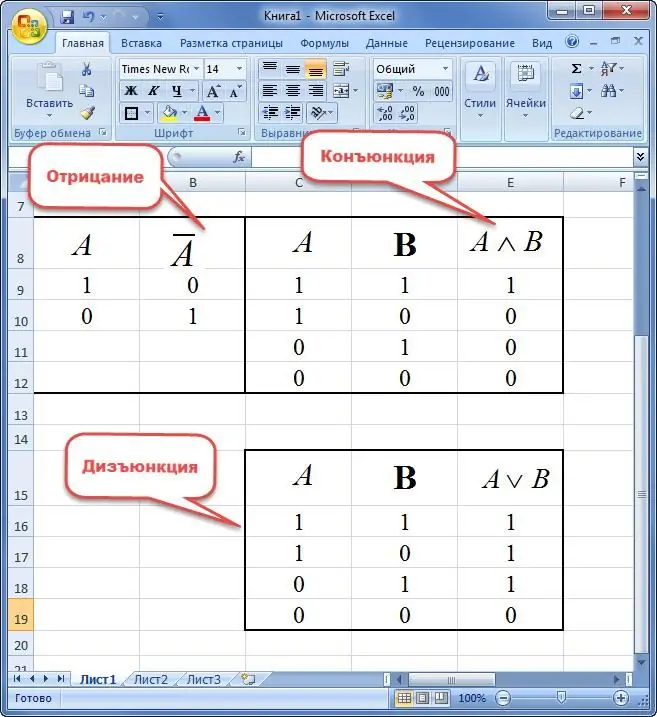
Negation är ett nytt uttryck som tar värdet av sant om det är falskt och vice versa.
Konjunktion av tvåvariabler kallas en ny mening, som tar värdet av sanning i fallet med samtidig beteckning "1" och falskhet i andra situationer.
Disjunktionen av två påståenden tolkas som ett nytt uttryck som tar värdet "FALSE" endast om det finns "0" och "TRUE" i andra varianter samtidigt.
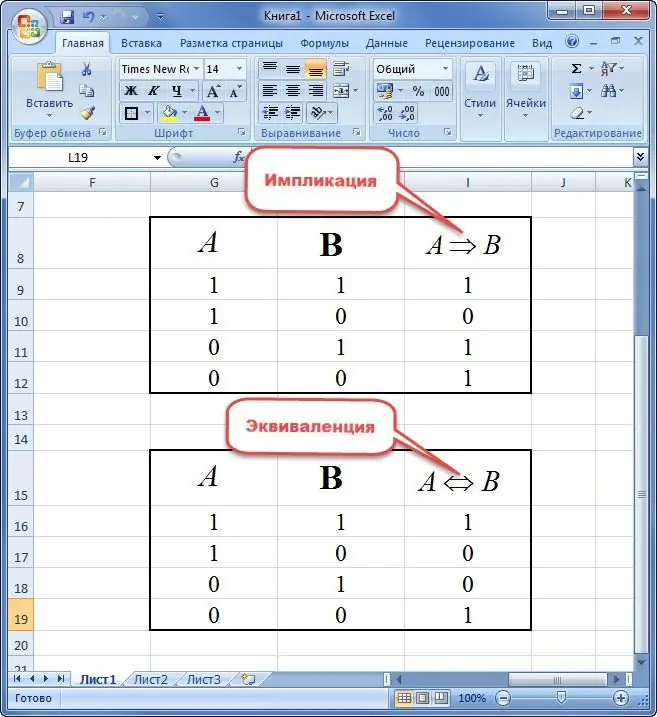
En implikation av två variabler är en ny mening där:
- om premissen är sann och konsekvensen är falsk, då är uttrycket lika med "0";
- sats är lika med "1" i andra fall.
Motsvarighet till två variabler förstås som ett nytt påstående som tar värdet av sanning endast om elementen är desamma. Annars är erbjudandet "0".
Logiska värden för uttryck presenteras vanligtvis i tabellform. Det finns ett annat namn för denna typ av information. De säger att för ett uttalande måste du bygga en sanningstabell. Den specificerar de initiala värdena för alla variabler och sedan beräknas resultatet av hela uttrycket.
Algorithm för implementering av beräkningar i logiska operationer
För att bygga en sanningstabell måste du veta i vilken ordning åtgärderna utförs. I ett uttryck med flera operander utförs beräkningen i följande ordning:
- inversion (negation);
- konjunktion (logisk funktion i Excel "AND");
- disjunction (boolesk operator i Excel "ELLER");
- implikation (konsekvens);
- ekvivalens.
Det finns ytterligare två operationer, men deras prioritet är inte definierad:
- Schaeffers stroke;
- Pierce-pil.
Beräkningsalgoritmen ändras om uttrycket omges av parentes.
Orden för att konstruera en tabellform för logiska operander i Excel
Innan du hittar värdet av ett uttryck måste du studera begreppet en logisk algebraformel. Definitionen säger att detta är ett komplext uttryck, som består av de enklaste påståendena sammankopplade med logiska operander.
Exempel 1. Konstruera en sanningstabell för konjunktion, disjunktion och negation.
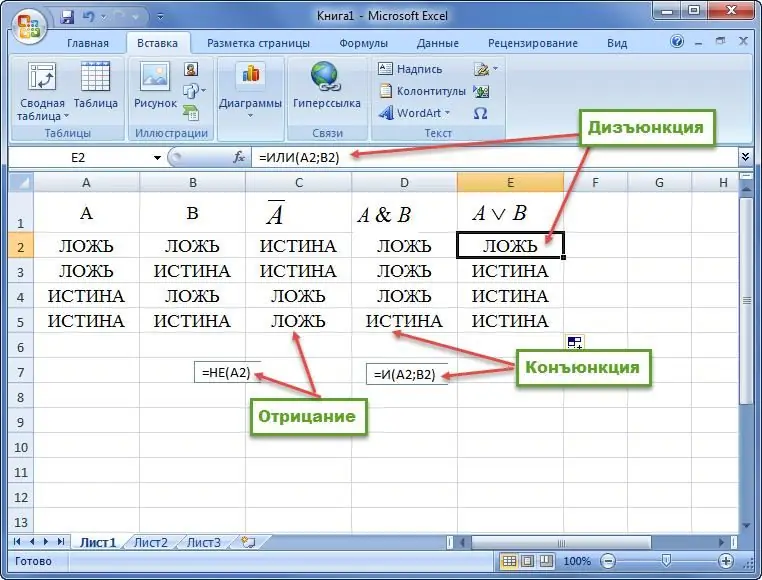
Exempel 2. Givet en formel för logikens algebra. Bygg en sanningstabell. Exempel exempel ges nedan.
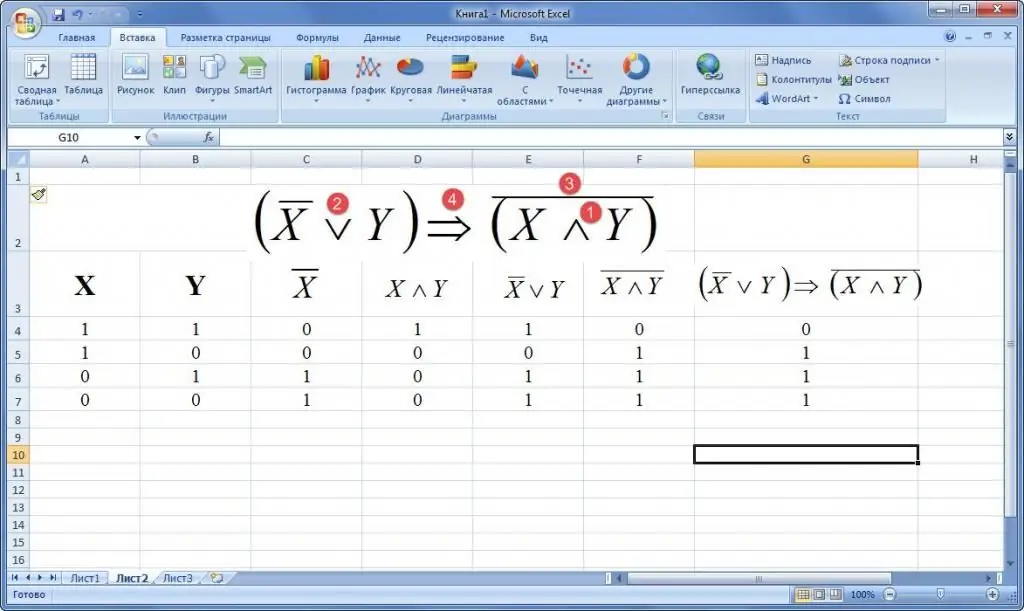
Exempel 3. Hur man bygger en sanningstabell i Excel, givet en formel för logisk algebra i en verbal beskrivning. Att säga: "Om en triangel är liksidig, så är alla dess kanter lika eller alla dess vinklar är lika."
Först måste du analysera den sammansatta meningen i minimala element:
- Första delen av uttrycket: A="liksidig triangel".
- Andra: B="alla sidor av figuren är lika".
- Tredje: C="alla vinklar i en triangel är lika".
Därefter kompileras ett uttryck och löses i Excel-programpaketet.
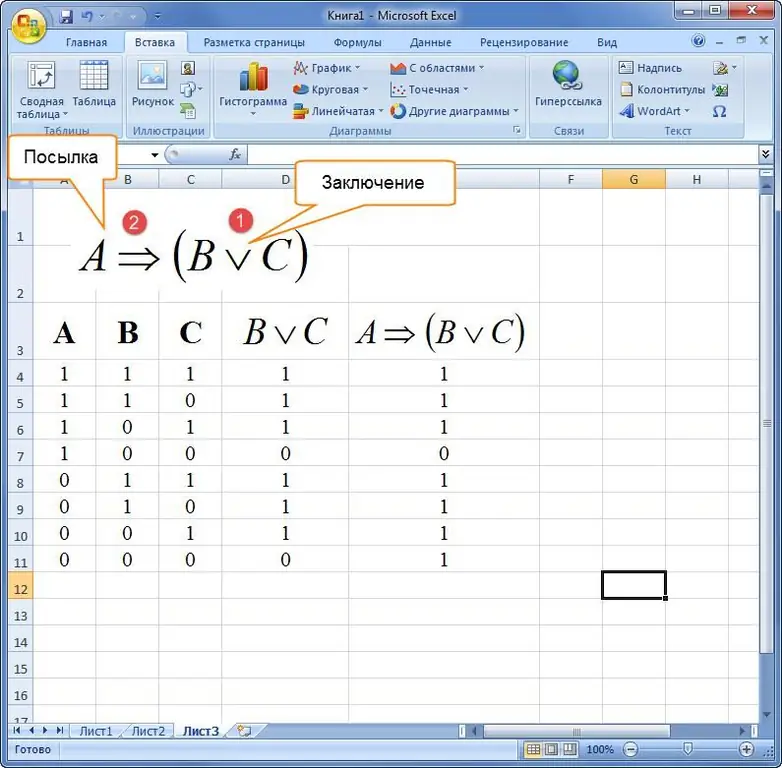
När man sammanställer sanningstabeller är det viktigt att komma ihåg operationsordningen.






