Gaser, ur termodynamikens synvinkel, beskrivs av en uppsättning makroskopiska egenskaper, varav de viktigaste är temperatur, tryck och volym. Konstansen för en av dessa parametrar och förändringen i de andra två indikerar att en eller annan isoprocess förekommer i gasen. Vi kommer att ägna den här artikeln till ett detaljerat svar på frågorna om att detta är en isokorisk process, hur den skiljer sig från isotermiska och isobariska förändringar i ett gassystems tillstånd.
Idealgas i fysik

Innan du svarar på frågan om att detta är en isokorisk process bör du lära känna konceptet med en idealgas bättre. Inom fysiken förstås det som vilken gas som helst där den genomsnittliga kinetiska energin för dess ingående partiklar vida överstiger den potentiella energin för deras interaktion, och avstånden mellan dessa partiklar är flera storleksordningar större än deras linjära dimensioner. Under de angivna förhållandena är det möjligt, när du utförberäkningar tar inte hänsyn till interaktionsenergin mellan partiklar (den är lika med noll), och det kan också antas att partiklarna är materialpunkter med en viss massa m.
Den enda processen som äger rum i en idealgas är kollisionen av partiklar med väggarna i kärlet som innehåller ämnet. Dessa kollisioner visar sig i praktiken som förekomsten av ett visst tryck i gasen P.
I regel kan varje gasformigt ämne som består av relativt kemiskt inerta molekyler och som har lågt tryck och höga temperaturer anses vara en idealisk gas med tillräcklig noggrannhet för praktiska beräkningar.
Ekvation som beskriver en idealisk gas
Vi talar naturligtvis om Clapeyron-Mendeleevs universella lag, som bör förstås väl för att förstå att detta är en isokorisk process. Så, den universella tillståndsekvationen har följande form:
PV=nRT.
Det vill säga produkten av trycket P och gasvolymen V är lika med produkten av den absoluta temperaturen T och mängden ämne i mol n, där R är proportionalitetsfaktorn. Själva ekvationen skrevs först ner av Emile Clapeyron 1834, och på 70-talet av 1800-talet ersatte D. Mendeleev i den en uppsättning konstanta värden av en enda universell gaskonstant R (8,314 J/(molK))).
I enlighet med Clapeyron-Mendeleev-ekvationen, i ett slutet system förblir antalet gaspartiklar konstant, så det finns bara tre makroskopiska parametrar som kan ändras (T, Poch V). Det senare faktumet ligger till grund för förståelsen av de olika isoprocesserna som kommer att diskuteras nedan.
Vad är en isokorisk process?
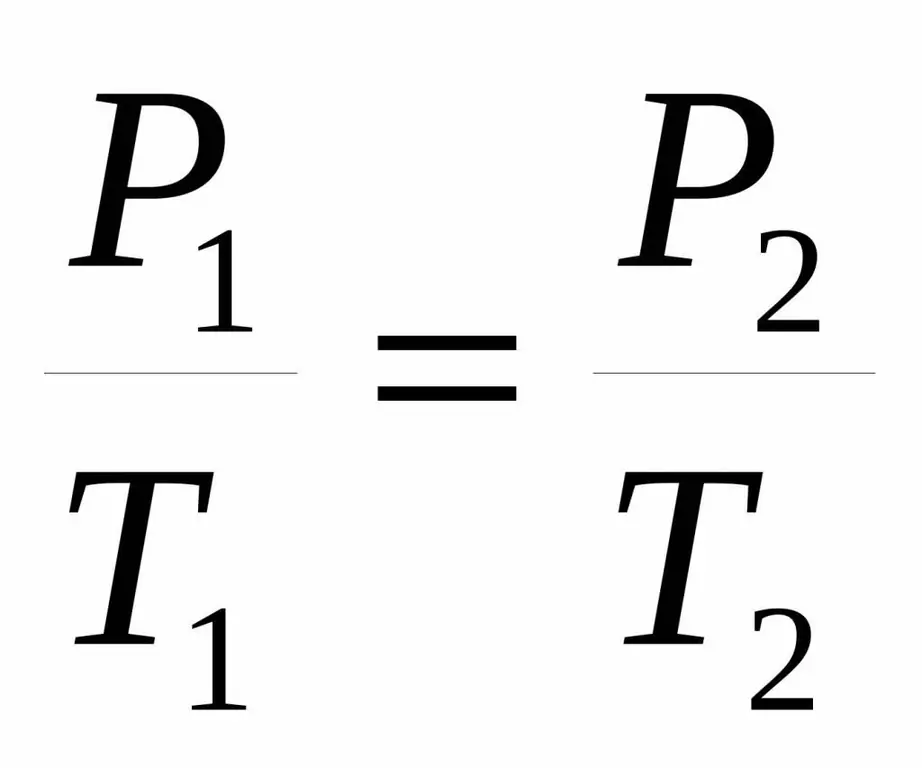
Denna process förstås som absolut varje förändring i systemets tillstånd, där dess volym bevaras.
Om vi vänder oss till den universella tillståndsekvationen kan vi säga att i en isokorisk process förändras endast tryck och absolut temperatur i en gas. För att förstå exakt hur de termodynamiska parametrarna förändras skriver vi motsvarande matematiska uttryck:
P / T=konst.
Ibland ges denna likhet i en något annorlunda form:
P1 / T1=P2 / T 2.
Båda jämlikheterna kallas Charles lag efter namnet på en fransk vetenskapsman som i slutet av 1700-talet erhöll det uppmärksammade beroendet experimentellt.

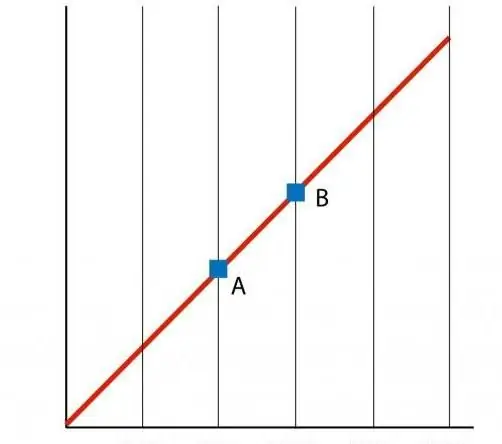
Om vi bygger en graf av funktionen P(T), så får vi ett rätlinjigt beroende, som kallas en isokor. Alla isokor (för alla värden på n och V) är en rak linje.
Energibeskrivning av processen
Som nämnts är en isokorisk process en förändring i tillståndet hos ett system som äger rum i ett slutet men inte isolerat system. Vi talar om möjligheten till värmeväxling mellan gasen och miljön. I allmänhet leder all tillförsel av värme Q till systemet till två resultat:
- ändrar intern energi U;
- gasfungerar A, expanderar eller drar ihop sig.
Den sista inferensen skrivs matematiskt enligt följande:
Q=U + A.
Den isokoriska processen för en idealgas, enligt dess definition, innebär inte arbete som utförs av gasen, eftersom dess volym förblir oförändrad. Det betyder att all värme som tillförs systemet går till att öka dess interna energi:
Q=U.
Om vi ersätter den explicita formeln för intern energi i detta uttryck, kan värmen från den isokoriska processen representeras som:
Q=z / 2nRT.
Här är z antalet frihetsgrader, som bestäms av den polyatomiska naturen hos molekylerna som utgör gasen. För en monoatomisk gas är z=3, för en diatomisk gas - 5, och för en triatomisk gas - 6. Här menar vi under frihetsgraderna translations- och rotationsgrader.
Om vi jämför effektiviteten av att värma ett gassystem i isokoriska och isobariska processer, så kommer vi i det första fallet att få maximal effektivitet, eftersom gasen expanderar under den isobariska förändringen i systemets tillstånd, och en del av värmetillförseln går åt till att utföra arbete.
Isobarisk process
Ovan har vi beskrivit i detalj att detta är en isokorisk process. Låt oss nu säga några ord om andra isoprocesser. Låt oss börja med isobar. Baserat på namnet förstås det som övergången av systemet mellan tillstånd vid konstant tryck. Denna process beskrivs av Gay-Lussac-lagen enligt följande:
V / T=konst.
Som med isokoren representerar V(T)-isobaren också en rak linje på grafen.
Förav alla isobariska processer är det lämpligt att beräkna det arbete som gasen utför, eftersom det är lika med produkten av konstant tryck och volymförändringen.
Isotermisk process
Detta är en process där temperaturen i systemet förblir konstant. Det beskrivs av Boyle-Mariottes lag för en idealisk gas. Det är märkligt att notera att detta är den första experimentellt upptäckta gaslagen (andra hälften av 1600-talet). Dess matematiska notation ser ut så här:
PV=konst.
Isokoriska och isotermiska processer skiljer sig åt vad gäller deras grafiska representation, eftersom funktionen P(V) är ett hyperboliskt, inte ett linjärt samband.
Exempel på problemlösning
Låt oss konsolidera den teoretiska informationen i artikeln genom deras tillämpning för att lösa ett praktiskt problem. Det är känt att rent gasformigt kväve fanns i en cylinder vid ett tryck på 1 atmosfär och en temperatur på 25 °C. Efter att gasflaskan värmts upp och trycket i den mätts visade det sig vara 1,5 atmosfärer. Vilken temperatur har gasen i cylindern efter uppvärmning? Hur mycket förändrades gasens inre energi om det fanns 4 mol kväve i ballongen.
För att svara på den första frågan använder vi följande uttryck:
P1 / T1=P2 / T 2.
Varifrån vi kommer:
T2=P2 / P1 T 1.
I detta uttryck kan tryck ersättas i godtyckliga enhetermätningar, eftersom de krymper, och temperaturen bara är i kelvin. Med det sagt får vi:
T2=1,5 /1298,15=447,224 K.
Den beräknade temperaturen i grader Celsius är 174 °C.
Eftersom kvävemolekylen är diatomisk kan förändringen i dess inre energi under uppvärmning bestämmas enligt följande:
ΔU=5 / 2nRΔT.
Genom att ersätta de kända värdena med detta uttryck får vi svaret på den andra frågan i problemet: ΔU=+12,4 kJ.






