Inom termodynamik är det viktigt att känna till den termiska effekten av processen när man studerar övergångar från det initiala till det slutliga tillståndet av ett system. Begreppet värmekapacitet är nära relaterat till denna effekt. I den här artikeln kommer vi att överväga frågan om vad som menas med en gass isokoriska värmekapacitet.
Ideal gas
En idealgas är en gas vars partiklar anses vara materiella punkter, det vill säga att de inte har dimensioner, utan har massa, och i vilken all inre energi enbart består av den kinetiska energin för molekylers rörelse och atomer.
Varje verklig gas som helst kommer aldrig att uppfylla den beskrivna modellen, eftersom dess partiklar fortfarande har några linjära dimensioner och interagerar med varandra genom att använda svaga van der Waals-bindningar eller kemiska bindningar av en annan typ. Men vid låga tryck och höga temperaturer är avstånden mellan molekylerna stora, och deras kinetiska energi överstiger den potentiella energin med dussintals gånger. Allt detta gör det möjligt att med en hög grad av noggrannhet applicera den idealiska modellen för riktiga gaser.
Gasens inre energi
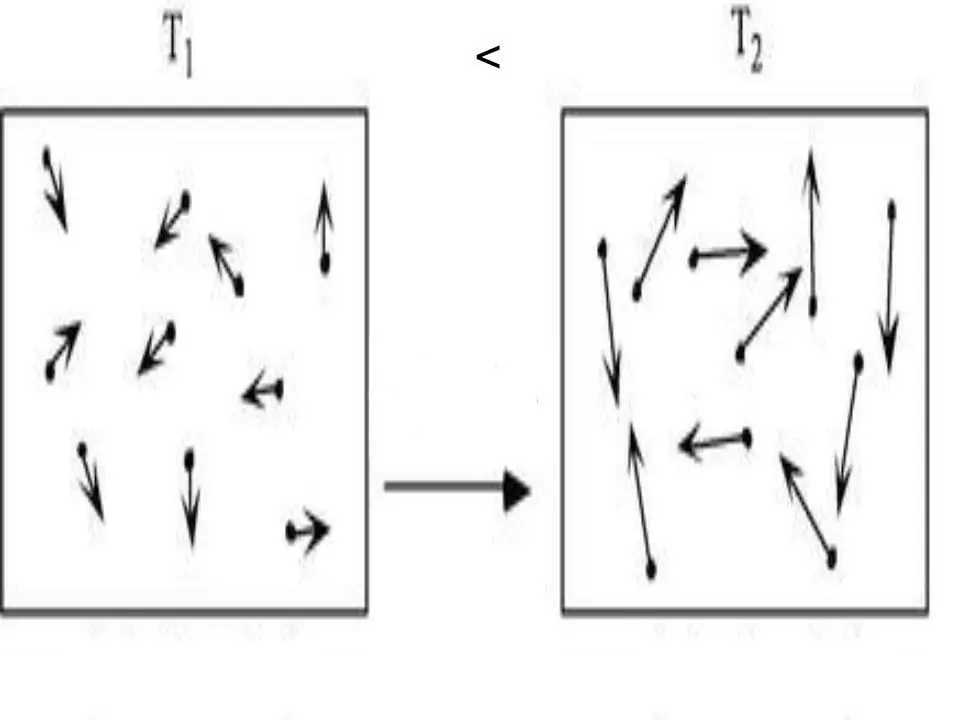
Den inre energin i vilket system som helst är en fysisk egenskap, som är lika med summan av potentiell och kinetisk energi. Eftersom potentiell energi kan försummas i idealgaser, kan vi skriva likheten för dem:
U=Ek.
Där Ek är det kinetiska systemets energi. Genom att använda den molekylära kinetiska teorin och tillämpa den universella Clapeyron-Mendeleev tillståndsekvationen är det inte svårt att få ett uttryck för U. Det står nedan:
U=z/2nRT.
Här är T, R och n den absoluta temperaturen, gaskonstanten respektive mängden ämne. z-värdet är ett heltal som anger antalet frihetsgrader som en gasmolekyl har.
Isobarisk och isokorisk värmekapacitet
Inom fysik är värmekapacitet den mängd värme som måste tillföras systemet som studeras för att värma det med en kelvin. Den omvända definitionen är också sant, det vill säga värmekapaciteten är den mängd värme som systemet avger när det kyls med en kelvin.
Det enklaste sättet för ett system är att bestämma den isokoriska värmekapaciteten. Det förstås som värmekapaciteten vid konstant volym. Eftersom systemet inte utför arbete under sådana förhållanden går all energi åt att öka interna energireserver. Låt oss beteckna den isokoriska värmekapaciteten med symbolen CV, då kan vi skriva:
dU=CVdT.
Det vill säga förändringen i intern energiSystemet är direkt proportionell mot förändringen i dess temperatur. Om vi jämför detta uttryck med likheten som skrevs i föregående stycke, kommer vi fram till formeln för CV i en idealgas:
СV=z/2nR.
Detta värde är obekvämt att använda i praktiken, eftersom det beror på mängden substans i systemet. Därför introducerades begreppet specifik isokorisk värmekapacitet, det vill säga ett värde som beräknas antingen per 1 mol gas eller per 1 kg. Låt oss beteckna det första värdet med symbolen CV, det andra - med symbolen CV m. För dem kan du skriva följande formler:
CV=z/2R;
CVm=z/2R/M.
Här är M molarmassan.
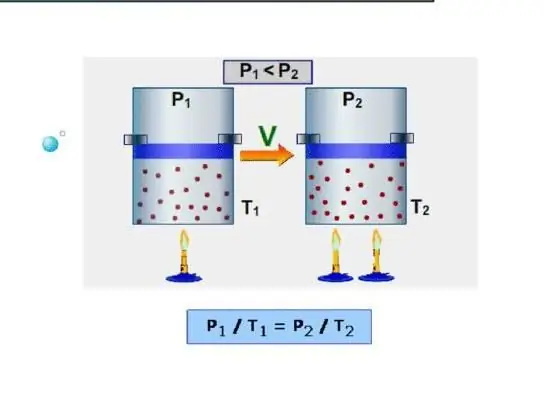
Isobarisk är värmekapaciteten samtidigt som ett konstant tryck i systemet bibehålls. Ett exempel på en sådan process är expansionen av gas i en cylinder under en kolv när den värms upp. Till skillnad från den isokoriska processen, används under den isobariska processen värmen som tillförs systemet för att öka den inre energin och för att utföra mekaniskt arbete, det vill säga:
H=dU + PdV.
Entalpin för en isobar process är produkten av den isobariska värmekapaciteten och temperaturförändringen i systemet, det vill säga:
H=CPdT.
Om vi betraktar expansionen vid ett konstant tryck på 1 mol gas, så kommer termodynamikens första lag att skrivas som:
CPdT=CV dT + RdT.
Den sista termen erhålls från ekvationenClapeyron-Mendeleev. Av denna jämlikhet följer förhållandet mellan isobarisk och isokorisk värmekapacitet:
CP=CV + R.
För en idealgas är den specifika molära värmekapaciteten vid konstant tryck alltid större än motsvarande isokoriska karakteristika med R=8, 314 J/(molK).
Frihetsgrader för molekyler och värmekapacitet
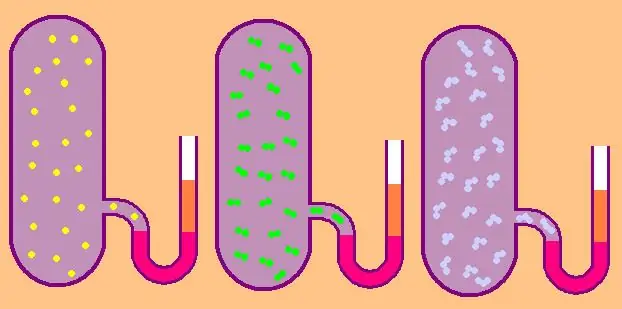
Låt oss återigen skriva formeln för den specifika molära isokoriska värmekapaciteten:
CV=z/2R.
I fallet med en monoatomisk gas är värdet z=3, eftersom atomer i rymden bara kan röra sig i tre oberoende riktningar.
Om vi talar om en gas som består av diatomiska molekyler, till exempel syre O2 eller väte H2, då, förutom translationell rörelse kan dessa molekyler fortfarande rotera runt två ömsesidigt vinkelräta axlar, det vill säga z kommer att vara lika med 5.
För mer komplexa molekyler, använd z=6. för att bestämma CV






