Värmekapaciteten hos en gas är mängden energi som en kropp absorberar när den värms upp med en grad. Låt oss analysera de viktigaste egenskaperna hos denna fysiska kvantitet.

Definitioner
En gass specifika värme är enhetsmassan för ett visst ämne. Dess måttenheter är J/(kg·K). Mängden värme som absorberas av kroppen i processen att ändra dess aggregationstillstånd är inte bara associerad med det initiala och slutliga tillståndet, utan också med övergångsmetoden.

Department
Värmekapaciteten hos gaser divideras med värdet bestämt vid konstant volym (Cv), konstant tryck (Cр).
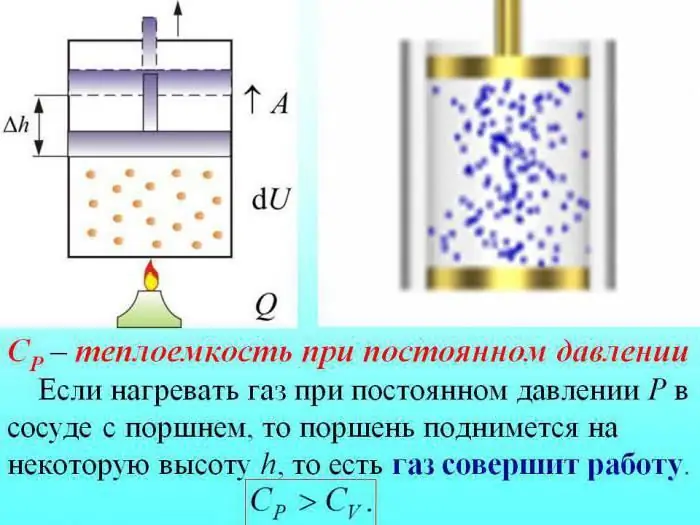
I fallet med uppvärmning utan att trycket ändras, används en del värme för att producera gasexpansion, och en del av energin används för att öka den inre energin.
Värmekapaciteten hos gaser vid konstant tryck bestäms av mängden värme som används för att öka intern energi.
Gasstatus: funktioner, beskrivning
Värmekapaciteten för en idealgas bestäms med hänsyn till det faktum att Сp-Сv=R. Den senare kvantiteten kallas den universella gaskonstanten. Dess värde motsvarar 8,314 J/(mol K).
När man gör teoretiska beräkningar av värmekapacitet, till exempel för att beskriva sambandet med temperatur, räcker det inte att endast använda termodynamiska metoder, det är viktigt att beväpna sig med element av statisk fysik.
Värmekapaciteten hos gaser involverar beräkning av medelvärdet av energin från translationsrörelsen hos vissa molekyler. Sådan rörelse sammanfattas från molekylens rotations- och translationsrörelse, såväl som från atomernas inre vibrationer.
Inom statisk fysik finns det information om att det för varje frihetsgrad av rotations- och translationsrörelse finns en kvantitet för en gas som är lika med hälften av den universella gaskonstanten.

Intressanta fakta
En partikel av en monoatomisk gas antas ha tre translationsfrihetsgrader, så det specifika värmet hos en gas har tre translations-, två rotations- och en vibrationsfrihetsgrader. Lagen för deras enhetliga fördelning leder till att det specifika värmet vid en konstant volym likställs med R.
Under experimenten fann man att värmekapaciteten hos en diatomisk gas motsvarar värdet R. En sådan diskrepans mellan teori och praktik förklaras av det faktum att värmekapaciteten hos en idealgas är förknippad med kvantum. effekter, när man gör beräkningar är det därför viktigt att använda statistik baserad på kvantummekanik.
Baserat på grunderna för kvantmekaniken har alla system av partiklar som oscillerar eller roterar, inklusive gasmolekyler, bara några diskreta energivärden.
Om energin från termisk rörelse i systemet inte räcker till för att excitera svängningar med en viss frekvens, bidrar sådana rörelser inte till systemets totala värmekapacitet.
Som ett resultat blir en specifik grad av frihet "fryst", det är omöjligt att tillämpa lagen om ekvipartition på den.
Värmekapaciteten hos gaser är en viktig egenskap hos det tillstånd som hela det termodynamiska systemets funktion beror på.
Temperaturen vid vilken ekvipartitionslagen kan tillämpas på vibrations- eller rotationsfrihetsgraden kännetecknas av kvantteorin, kopplar samman Planck-konstanten med Boltzmann-konstanten.

Diatomiska gaser
Gapet mellan rotationsenerginivåerna för sådana gaser är ett litet antal grader. Undantaget är väte, där temperaturvärdet bestäms av hundratals grader.
Det är därför värmekapaciteten hos en gas vid konstant tryck är svår att beskriva med lagen om likformig fördelning. I kvantstatistiken, när man bestämmer värmekapaciteten, tar man hänsyn till att dess vibrationsdel, vid en temperatursänkning, snabbt minskar och når noll.
Detta fenomen förklarar det faktum att vid rumstemperatur finns det praktiskt taget ingen vibrationsdel av värmekapaciteten, t.ex.diatomisk gas, motsvarar den konstanten R.
Värmekapaciteten för en gas vid konstant volym vid lågtemperaturindikatorer bestäms med hjälp av kvantstatistik. Det finns Nernst-principen, som kallas termodynamikens tredje lag. Baserat på dess formulering kommer den molära värmekapaciteten hos en gas att minska med sjunkande temperatur och tenderar till noll.

Features of solids
Om värmekapaciteten hos en blandning av gaser kan förklaras med hjälp av kvantstatistik, så kännetecknas termisk rörelse för ett fast aggregationstillstånd av små fluktuationer av partiklar nära jämviktspositionen.
Varje atom har tre vibrationsgrader av frihet, därför kan, i enlighet med ekvipartitionslagen, den molära värmekapaciteten för ett fast ämne beräknas som 3nR, där n är antalet atomer i en molekyl.
I praktiken är denna siffra gränsen som värmekapaciteten hos en fast kropp tenderar till vid höga temperaturer.
Maximal kan erhållas vid vanliga temperaturer för vissa grundämnen, inklusive metaller. För n=1 är Dulong- och Petit-lagen uppfyllda, men för komplexa ämnen är det ganska svårt att nå en sådan gräns. Eftersom gränsen inte kan erhållas i verkligheten sker nedbrytning eller smältning av det fasta ämnet.
History of quantum theory
Grundarna av kvantteorin är Einstein och Debye i början av 1900-talet. Den är baserad på kvantisering av oscillerande rörelser hos atomer i en visskristall. När det gäller lågtemperaturindikatorer visar sig värmekapaciteten hos en fast kropp vara direkt proportionell mot det absoluta värdet i kuber. Detta förhållande har kallats Debyes lag. Som ett kriterium som gör det möjligt att skilja mellan låg- och högtemperaturindikatorer tas deras jämförelse med Debye-temperaturen.
Detta värde bestäms av spektrumet av vibrationer för en atom i kroppen, därför beror det allvarligt på egenskaperna hos dess kristallstruktur.
QD är ett värde som har flera hundra K, men det är till exempel mycket högre i diamant.
Ledningselektronerna ger ett betydande bidrag till metallernas värmekapacitet. För att beräkna det används Fermi-kvantstatistiken. Den elektroniska konduktiviteten för metallatomer är direkt proportionell mot den absoluta temperaturen. Eftersom det är ett obetydligt värde, beaktas det endast vid temperaturer som tenderar till absolut noll.
Metoder för att bestämma värmekapacitet
Den huvudsakliga experimentella metoden är kalorimetri. För att genomföra en teoretisk beräkning av värmekapacitet används statistisk termodynamik. Det är giltigt för en ideal gas, såväl som för kristallina kroppar, utförs på grundval av experimentella data om strukturen av materia.
Empiriska metoder för att beräkna värmekapaciteten hos en idealgas är baserade på idén om den kemiska strukturen, bidraget från enskilda grupper av atomer till Ср.
För vätskor används även metoder som bygger på användning av termodynamiskcykler som gör det möjligt att passera från värmekapaciteten hos en idealgas till en vätska genom derivatan av temperaturen i entalpin för förångningsprocessen.
I fallet med en lösning är beräkningen av värmekapaciteten som en additiv funktion inte tillåten, eftersom övervärdet av lösningens värmekapacitet i princip är signifikant.
För att utvärdera det behöver vi den molekylärstatistiska teorin om lösningar. Det svåraste är identifieringen av värmekapaciteten hos heterogena system i termodynamisk analys.

Slutsats
Studien av värmekapacitet låter dig beräkna energibalansen för processer som sker i kemiska reaktorer, såväl som i andra kemiska produktionsapparater. Dessutom är detta värde nödvändigt för valet av optimala typer av kylmedel.
För närvarande är den experimentella bestämningen av ämnens värmekapacitet för olika temperaturintervall - från låga värden till höga värden - huvud alternativet för att bestämma ett ämnes termodynamiska egenskaper. Vid beräkning av ett ämnes entropi och entalpi används värmekapacitetsintegraler. Information om värmekapaciteten hos kemiska reagenser i ett visst temperaturintervall gör att du kan beräkna processens termiska effekt. Information om lösningars värmekapacitet gör det möjligt att beräkna deras termodynamiska parametrar vid valfria temperaturvärden inom det analyserade intervallet.
En vätska kännetecknas till exempel av att en del av värmen förbrukas för att ändra värdet på potentiell energireagerande molekyler. Detta värde kallas "konfigurations" värmekapacitet, används för att beskriva lösningar.
Det är svårt att göra fullfjädrade matematiska beräkningar utan att ta hänsyn till ett ämnes termodynamiska egenskaper, dess aggregationstillstånd. Det är därför som för vätskor, gaser, fasta ämnen används en sådan egenskap som specifik värmekapacitet, vilket gör det möjligt att karakterisera energiparametrarna för ett ämne.






