När man studerar i fysik den mekaniska rörelsen hos kroppar i rymden, tar de alltid hänsyn till den resulterande accelerationen. Låt oss i artikeln överväga vad acceleration är och hur det betecknas i fysiken, och även lösa ett enkelt problem för att beräkna detta värde.
Vad är acceleration och vilka är dess typer?
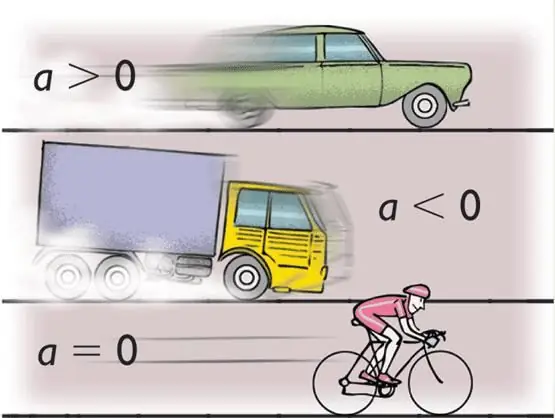
Under accelerationen förstå värdet, vars betydelse är hastigheten för förändring av kroppens hastighet. Matematiskt skrivs denna definition på följande sätt:
a=dv/dt.
Om tidsfunktionen för hastighet är känd räcker det med att hitta dess första derivata för att beräkna accelerationen vid en given tidpunkt.
I fysiken är accelerationsbokstaven den gemena latinska a. Detta är dock den så kallade linjära accelerationen, som mäts i enheter m/s2. Utöver det finns det också vinkelacceleration. Den visar förändringen i vinkelhastighet och uttrycks i enheter av rad/s2. Denna typ av acceleration betecknas med den grekiska gemena bokstaven α (alfa). Iblandbokstaven ε (epsilon) används för att beteckna den.
Om kroppen rör sig längs en krökt bana, delas den totala accelerationen upp i två komponenter: tangentiell (bestämmer hastighetsändringen i storlek) och normal (bestämmer hastighetsändringen i riktning). Dessa typer av acceleration betecknas också med bokstäverna a, men med motsvarande index: at och a. Normal kallas ofta centripetal, och tangentiell kallas ofta tangent.
Äntligen finns det en annan typ av acceleration som uppstår när kroppar faller fritt i planetens gravitationsfält. Det betecknas med bokstaven g.
Problem i fysik för acceleration
Det är känt att kroppen rör sig i en rak linje. Dess hastighet över tiden bestäms av följande lag:
v=2t2-t+4.
Det är nödvändigt att beräkna accelerationen som kroppen kommer att ha vid tiden t=2,5 sekunder.
Efter definitionen av a får vi:
a=dv/dt=4t - 1.
Det vill säga att värdet a beror linjärt på tiden. Det är märkligt att notera att i det initiala ögonblicket (t=0) var accelerationen negativ, det vill säga riktad mot hastighetsvektorn. Vi får svaret på problemet genom att ersätta t=2,5 sekunder i denna ekvation: a=9 m/s2.






