Upplösning är förmågan hos ett bildsystem att återge detaljerna i ett objekt, och beror på faktorer som typen av belysning som används, sensorns pixelstorlek och optikens kapacitet. Ju mindre detalj motivet är, desto högre krävs objektivets upplösning.
Introduktion till lösningsprocessen
Kamerans bildkvalitet beror på sensorn. Enkelt uttryckt är en digital bildsensor ett chip inuti ett kamerahus som innehåller miljontals ljuskänsliga fläckar. Storleken på en kamerans sensor avgör hur mycket ljus som kan användas för att skapa en bild. Ju större sensor, desto bättre bildkvalitet eftersom mer information samlas in. Vanligtvis annonserar digitalkameror på marknaden för sensorstorlekar på 16 mm, Super 35 mm och ibland upp till 65 mm.
När storleken på sensorn ökar kommer skärpedjupet att minska vid en given bländare, eftersom en större motsvarighet kräver att du kommer närmareobjekt eller använd en längre brännvidd för att fylla ramen. För att behålla samma skärpedjup måste fotografen använda mindre bländare.
Detta korta skärpedjup kan vara önskvärt, särskilt för att få bakgrundsoskärpa för porträtt, men landskapsfotografering kräver mer djup, vilket är lättare att fånga med den flexibla bländarstorleken hos kompaktkameror.
Att dividera antalet horisontella eller vertikala pixlar på en sensor indikerar hur mycket utrymme var och en upptar på ett objekt, och kan användas för att utvärdera linsens upplösningsförmåga och lösa kundernas problem angående enhetens digitala bildpixelstorlek. Som utgångspunkt är det viktigt att förstå vad som faktiskt kan begränsa systemets upplösning.
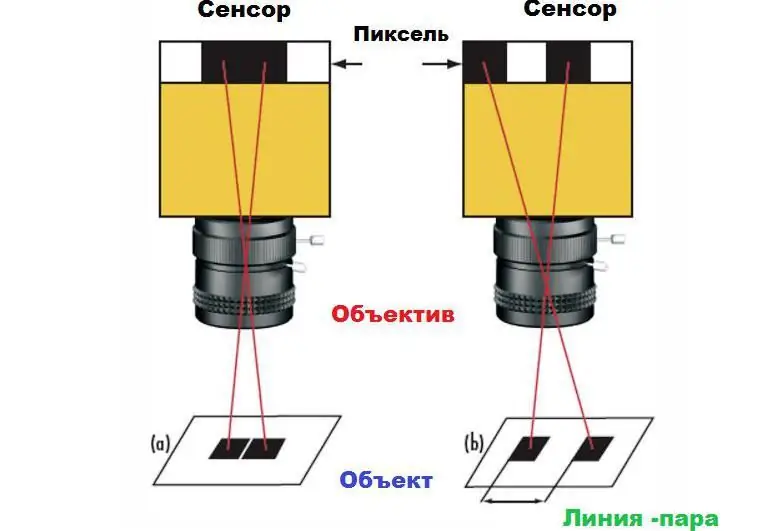
Detta påstående kan demonstreras med exemplet med ett par rutor på en vit bakgrund. Om kvadraterna på kamerasensorn är mappade till angränsande pixlar, kommer de att visas som en stor rektangel i bilden (1a) snarare än två separata kvadrater (1b). För att särskilja rutorna krävs ett visst mellanrum mellan dem, minst en pixel. Detta minsta avstånd är systemets maximala upplösning. Den absoluta gränsen bestäms av storleken på pixlarna på sensorn, såväl som deras antal.
Mätlinsegenskaper
Släktskapet mellan omväxlande svarta och vita rutor beskrivs som ett linjärt par. Vanligtvis bestäms upplösningen av frekvensen,mätt i linjepar per millimeter - lp/mm. Tyvärr är objektivets upplösning i cm inte ett absolut tal. Vid en given upplösning kommer möjligheten att se de två kvadraterna som separata objekt att bero på gråskalenivån. Ju större gråskaleavståndet är mellan dem och rymden, desto stabilare är förmågan att lösa dessa rutor. Denna uppdelning av gråskalan kallas frekvenskontrast.
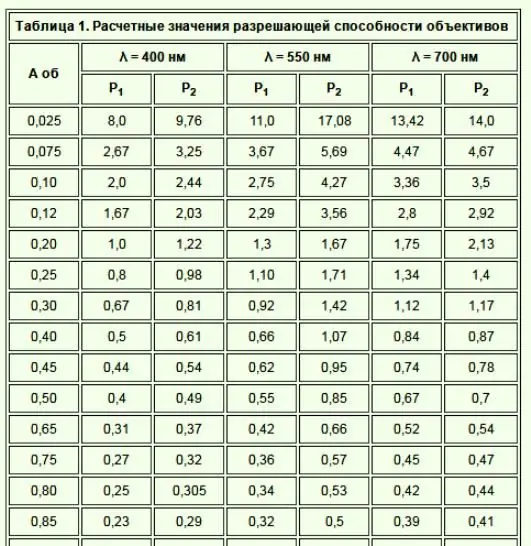
Spatial frekvens anges i lp/mm. Av denna anledning är det extremt användbart att beräkna upplösning i termer av lp/mm när man jämför linser och bestämmer det bästa valet för givna sensorer och applikationer. Den första är där systemupplösningsberäkningen börjar. Från och med sensorn är det lättare att avgöra vilka linsspecifikationer som behövs för att uppfylla kraven för enheten eller andra applikationer. Den högsta frekvensen som sensorn tillåter, Nyquist, är i praktiken två pixlar eller ett linjepar.
Definitionslinsupplösning, även kallad systembildsupplösning, kan bestämmas genom att multiplicera storleken i Μm med 2 för att skapa ett par och dividera med 1000 för att konvertera till mm:
lp/mm=1000/ (2 X pixel)
Sensorer med större pixlar kommer att ha lägre upplösningsgränser. Sensorer med mindre pixlar presterar bättre enligt linsupplösningsformeln ovan.
Aktivt sensorområde
Du kan beräkna den maximala upplösningen för objektetvisning. För att göra detta är det nödvändigt att skilja mellan indikatorer som förhållandet mellan storleken på sensorn, synfältet och antalet pixlar på sensorn. Storleken på den senare hänvisar till parametrarna för kamerasensorns aktiva område, vanligtvis bestäms av storleken på dess format.
De exakta proportionerna kommer dock att variera beroende på bildförhållande, och nominella sensorstorlekar bör endast användas som riktlinje, särskilt för telecentriska objektiv och höga förstoringar. Sensorstorleken kan beräknas direkt från pixelstorleken och antalet aktiva pixlar för att utföra objektivets upplösningstest.
Tabellen visar Nyquist-gränsen för pixelstorlekar som finns på några mycket vanliga sensorer.
| Pixelstorlek (µm) | Coupled Nyquist limit (lp / mm) |
| 1, 67 | 299, 4 |
| 2, 2 | 227, 3 |
| 3, 45 | 144, 9 |
| 4, 54 | 110, 1 |
| 5, 5 | 90, 9 |
När pixelstorlekarna minskar, ökar den associerade Nyquist-gränsen i lp/mm proportionellt. För att bestämma den absoluta minsta upplösningsbara fläck som kan ses på ett föremål, måste förhållandet mellan synfältet och storleken på sensorn beräknas. Detta är också känt som primär augmentation.(PMAG) system.
Förhållandet som är associerat med systemet PMAG tillåter skalning av bildutrymmets upplösning. När man utformar en applikation specificeras den vanligtvis inte i lp/mm, utan snarare i mikron (µm) eller bråkdelar av en tum. Du kan snabbt hoppa till den ultimata upplösningen för ett objekt genom att använda formeln ovan för att göra det lättare att välja objektivupplösning z. Det är också viktigt att komma ihåg att det finns många ytterligare faktorer, och ovanstående begränsning är mycket mindre felbenägen än komplexiteten i att ta hänsyn till många faktorer och beräkna dem med hjälp av ekvationer.
Beräkna brännvidd
Upplösningen för en bild är antalet pixlar i den. Designad i två dimensioner, till exempel 640X480. Beräkningar kan göras separat för varje dimension, men för enkelhets skull reduceras detta ofta till en. För att göra exakta mätningar på en bild måste du använda minst två pixlar för varje minsta område du vill upptäcka. Sensorns storlek hänvisar till en fysisk indikator och anges som regel inte i passdata. Det bästa sättet att bestämma storleken på en sensor är att titta på pixelparametrarna på den och multiplicera den med bildförhållandet, i vilket fall linsens upplösningsförmåga löser problemen med ett dåligt skott.
Till exempel har Basler acA1300-30um-kameran en pixelstorlek på 3,75 x 3,75 um och en upplösning på 1296 x 966 pixlar. Sensorns storlek är 3,75 µm x 1296 x 3,75 µm x 966=4,86 x 3,62 mm.
Sensorformat hänvisar till den fysiska storleken och beror inte på pixelstorleken. Denna inställning används föravgöra vilket objektiv kameran är kompatibel med. För att de ska matcha måste linsformatet vara större än eller lika med sensorstorleken. Om ett objektiv med ett mindre bildförhållande används kommer bilden att uppleva vinjettering. Detta gör att områden på sensorn utanför kanten av linsformatet blir mörka.
Pixel och kameraval

För att se objekten i bilden måste det finnas tillräckligt med utrymme mellan dem så att de inte smälter samman med närliggande pixlar, annars går de inte att skilja från varandra. Om objekten är en pixel var måste separationen mellan dem också vara minst ett element, det är tack vare detta som ett par linjer bildas, som egentligen har två pixlar i storlek. Detta är en av anledningarna till att det är felaktigt att mäta upplösningen på kameror och objektiv i megapixlar.
Det är faktiskt lättare att beskriva ett systems upplösningsförmåga i termer av linjeparfrekvens. Det följer att när pixelstorleken minskar, ökar upplösningen eftersom du kan placera mindre objekt på mindre digitala element, ha mindre utrymme mellan dem och fortfarande lösa avståndet mellan motiven du fotograferar.
Detta är en förenklad modell av hur kamerans sensor känner av objekt utan att ta hänsyn till brus eller andra parametrar, och är den idealiska situationen.
MTF-kontrastdiagram
De flesta linser är inte perfekta optiska system. Ljus som passerar genom en lins genomgår en viss grad av nedbrytning. Frågan är hur man ska värdera dettadegradering? Innan du besvarar denna fråga är det nödvändigt att definiera begreppet "modulering". Det senare är ett mått på kontrasten len vid en given frekvens. Man skulle kunna försöka analysera verkliga bilder tagna genom en lins för att bestämma modulering eller kontrast för detaljer av olika storlekar eller frekvenser (mellanrum), men detta är mycket opraktiskt.
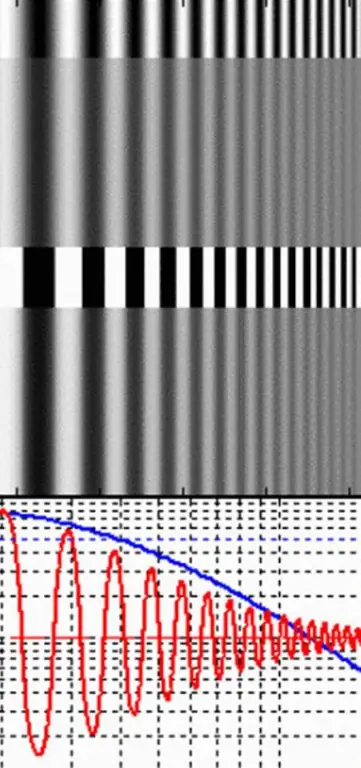
Istället är det mycket lättare att mäta modulering eller kontrast för par av omväxlande vita och mörka linjer. De kallas rektangulärt gitter. Intervallet för linjer i ett rektangulärt våggitter är frekvensen (v), för vilken linsens modulations- eller kontrastfunktion och upplösningen mäts i cm.
Den maximala mängden ljus kommer från de ljusa banden och minsta från de mörka banden. Om ljus mäts i termer av ljusstyrka (L), kan moduleringen bestämmas enligt följande ekvation:
modulation=(Lmax - Lmin) / (Lmax + Lmin), där: Lmax är den maximala ljusstyrkan för vita linjer i gittret, och Lmin är den lägsta ljusstyrkan för mörka.
När modulering definieras i termer av ljus, kallas det ofta för Michelson-kontrast eftersom det tar förhållandet mellan luminans från ljusa och mörka band för att mäta kontrast.
Till exempel finns det ett fyrkantsvågsgitter med en viss frekvens (v) och modulering, och en inneboende kontrast mellan mörka och ljusa områden som reflekteras från detta gitter genom linsen. Bildmodulering och därmed linskontrast mäts för en given frekvenstakter (v).
Modulationsöverföringsfunktionen (MTF) definieras som moduleringen M i av bilden dividerat med moduleringen av stimulus (objekt) M o, som visas i följande ekvation.
|
MTF (v)=M i / M 0 |
USF-testrutnät är tryckta på 98 % ljust laserpapper. Svart laserskrivartoner har en reflektans på cirka 10 %. Så värdet för M 0 är 88 %. Men eftersom film har ett mer begränsat dynamiskt omfång jämfört med det mänskliga ögat, är det säkert att anta att M 0 i huvudsak är 100 % eller 1. Så ovanstående formel kokar ner till följande mer enkel ekvation:
|
MTF (v)=Mi |
Så MTF-linsen för en given gitterfrekvens (v) är helt enkelt den uppmätta gittermodulationen (Mi) när den fotograferas genom en lins på film.
Mikroskopupplösning
Upplösningen för ett mikroskopobjektiv är det kortaste avståndet mellan två distinkta punkter i okularets synfält som fortfarande kan särskiljas som olika objekt.
Om två punkter är närmare varandra än din upplösning kommer de att verka otydliga och deras positioner blir felaktiga. Mikroskopet kan ge hög förstoring, men om linserna är av dålig kvalitet kommer den resulterande dåliga upplösningen att försämra bildkvaliteten.
Nedan är Abbe-ekvationen, där upplösningenstyrkan för ett mikroskopobjektiv z är upplösningsförmågan lika med våglängden för det använda ljuset dividerat med 2 (objektivets numeriska bländare).
Flera element påverkar upplösningen i ett mikroskop. Ett optiskt mikroskop inställt på hög förstoring kan producera en bild som är suddig, men den har fortfarande objektivets maximala upplösning.
Den digitala bländaren på ett objektiv påverkar upplösningen. Upplösningsförmågan hos ett mikroskopobjektiv är ett tal som indikerar förmågan hos en lins att samla ljus och lösa upp en punkt på ett fast avstånd från objektivet. Den minsta punkten som kan lösas upp av linsen är proportionell mot våglängden för det insamlade ljuset dividerat med det numeriska bländartalet. Därför motsvarar ett större antal en större förmåga hos linsen att upptäcka en utmärkt punkt i synfältet. Linsens numeriska bländare beror också på mängden optisk aberrationskorrigering.
upplösning för teleskoplinsen
Som en ljustratt kan ett teleskop samla ljus i proportion till hålets yta, den här egenskapen är huvudlinsen.
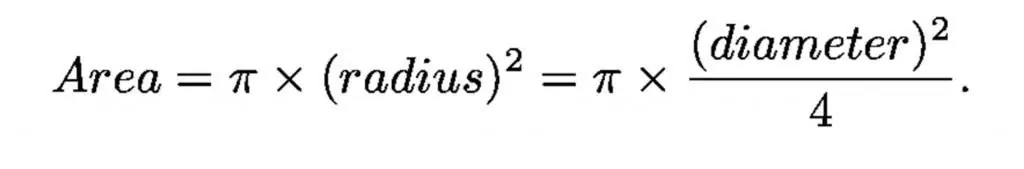
Diametern på det mänskliga ögats mörkt anpassade pupill är strax under 1 centimeter, och diametern på det största optiska teleskopet är 1 000 centimeter (10 meter), så att det största teleskopet är en miljon gånger större i samlingen område än det mänskliga ögat.

Det är därför teleskop ser svagare föremål än människor. Och har enheter som samlar ljus med hjälp av elektroniska detekteringssensorer i många timmar.
Det finns två huvudtyper av teleskop: linsbaserade refraktorer och spegelbaserade reflektorer. Stora teleskop är reflektorer eftersom speglar inte behöver vara genomskinliga. Teleskopspeglar är bland de mest exakta designerna. Det tillåtna felet på ytan är ungefär 1/1000 av bredden på ett människohår - genom ett 10 meters hål.
Speglar brukade vara gjorda av enorma tjocka glasskivor för att hålla dem från att hänga. Dagens speglar är tunna och flexibla, men är datorstyrda eller på annat sätt segmenterade och inriktade med datorstyrning. Förutom uppgiften att hitta svaga föremål är astronomens mål också att se deras fina detaljer. Graden i vilken detaljer kan kännas igen kallas upplösning:
- Luddiga bilder=dålig upplösning.
- Klara bilder=bra upplösning.
På grund av ljusets vågnatur och fenomen som kallas diffraktion, begränsar diametern på ett teleskops spegel eller lins dess slutliga upplösning i förhållande till teleskopets diameter. Upplösningen här betyder den minsta vinklade detalj som kan kännas igen. Små värden motsvarar utmärkt bilddetaljer.
Radioteleskop måste vara mycket stora för att ge bra upplösning. Jordens atmosfär ärturbulenta och suddiga teleskopbilder. Terrestra astronomer kan sällan nå apparatens maximala upplösning. Atmosfärens turbulenta effekt på en stjärna kallas syn. Denna turbulens får stjärnorna att "glitra". För att undvika dessa atmosfäriska oskärpa skjuter astronomer upp teleskop i rymden eller placerar dem på höga berg med stabila atmosfäriska förhållanden.
Exempel på parameterberäkning
Data för att bestämma Canon-objektivupplösning:
- Pixelstorlek=3,45 µm x 3,45 µm.
- Pixel (H x V)=2448 x 2050.
- Önskat synfält (horisontellt)=100 mm.
- Sensorupplösningsgräns: 1000/2x3, 45=145 lp/mm.
- Sensormått:3,45x2448/1000=8,45 mm3, 45x2050/1000=7,07 mm.
- PMAG:8, 45/100=0,0845 mm.
- Linsupplösning: 145 x 0,0845=12,25 lp/mm.
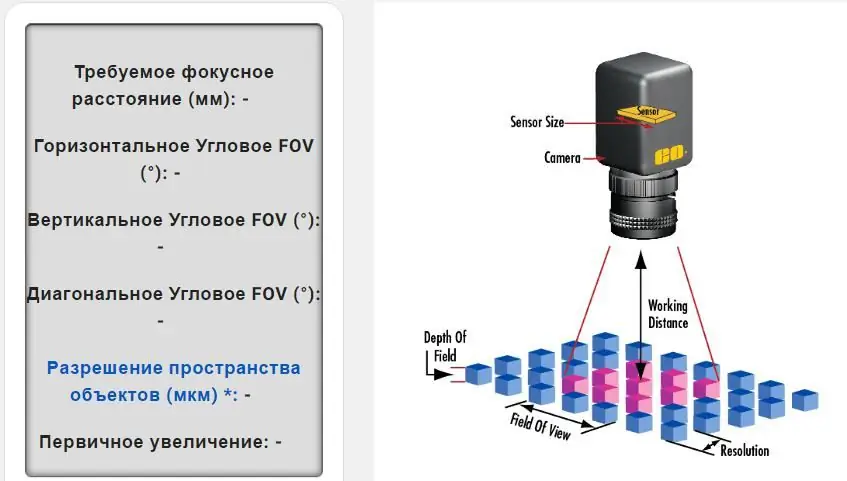
De här beräkningarna är faktiskt ganska komplexa, men de hjälper dig att skapa en bild baserad på sensorstorlek, pixelformat, arbetsavstånd och synfält i mm. Genom att beräkna dessa värden avgörs det bästa objektivet för dina bilder och applikation.
Problem med modern optik

Tyvärr skapar en fördubbling av storleken på sensorn ytterligare problem för linser. En av de viktigaste parametrarna som påverkar kostnaden för ett bildobjektiv är formatet. Att designa ett objektiv för en sensor i större format krävermånga individuella optiska komponenter, som borde vara större och överföringen av systemet stelare.
Ett objektiv designat för en 1"-sensor kan kosta fem gånger så mycket som ett objektiv designat för en ½"-sensor, även om det inte kan använda samma specifikationer med begränsad pixelupplösning. Kostnadskomponenten måste övervägas innan hur för att bestämma upplösningsförmågan hos en lins.
Optisk bildhantering står idag inför fler utmaningar än för ett decennium sedan. Sensorerna de används med har mycket högre upplösningskrav, och formatstorlekar drivs samtidigt både mindre och större, samtidigt som pixelstorleken fortsätter att krympa.
Förr begränsade optiken aldrig bildsystemet, idag gör det det. Där en typisk pixelstorlek är runt 9 µm, är en mycket vanligare storlek runt 3 µm. Den här 81x ökningen av punktdensitet har tagit ut sin rätt på optiken, och även om de flesta enheter är bra, är linsval nu viktigare än någonsin.






