Ohms lag i differential- och integralform säger att strömmen genom en ledare mellan två punkter är direkt proportionell mot spänningen i de två punkterna. En ekvation med en konstant ser ut så här:
I=V/R, där I är punkten för strömmen genom ledaren i enheter av ampere, V (Volt) är spänningen mätt med ledaren i enheter av volt, R är resistansen hos materialet som leds i ohm. Mer specifikt säger Ohms lag att R är en konstant i detta avseende, oberoende av ström.
Vad kan förstås med "Ohms lag"?
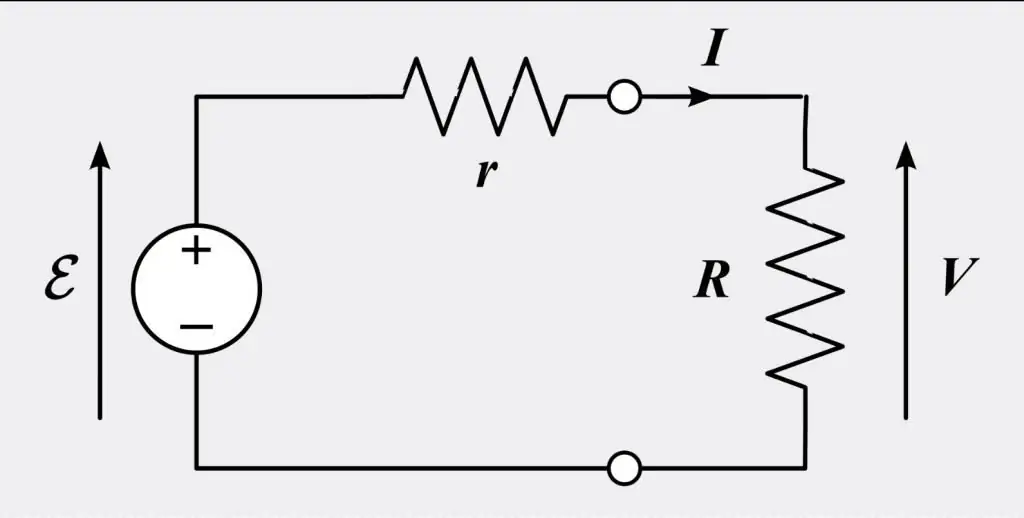
Ohms lag i differential- och integralform är ett empiriskt förhållande som exakt beskriver ledningsförmågan hos de allra flesta ledande material. Vissa material följer dock inte Ohms lag, de kallas "nonohmic". Lagen fick sitt namn efter vetenskapsmannen Georg Ohm, som publicerade den 1827. Den beskriver spännings- och strömmätningar med hjälp av enkla elektriska kretsar som innehållerolika trådlängder. Ohm förklarade sina experimentella resultat med en något mer komplex ekvation än den moderna formen ovan.
Begreppet Ohms lag i diff. form används också för att beteckna olika generaliseringar, till exempel används dess vektorform inom elektromagnetism och materialvetenskap:
J=σE, där J är antalet elektriska partiklar på ett visst ställe i det resistiva materialet, e är det elektriska fältet på den platsen och σ (sigma) är det material som är beroende av konduktivitetsparametern. Gustav Kirchhoff formulerade lagen exakt så här.
Historia

Historia
I januari 1781 experimenterade Henry Cavendish med en Leyden-burk och ett glasrör med olika diametrar fyllt med en s altlösning. Cavendish skrev att hastigheten ändras direkt som graden av elektrifiering. Till en början var resultaten okända för forskarvärlden. Men Maxwell publicerade dem 1879.
Ohm gjorde sitt arbete med motstånd 1825 och 1826 och publicerade sina resultat 1827 i "The Galvanic Circuit Proved Mathematically". Han inspirerades av den franske matematikern Fouriers arbete, som beskrev värmeledning. För experiment använde han till en början galvaniska pålar, men bytte senare till termoelement, som kunde ge en mer stabil spänningskälla. Han arbetade med begreppen internt motstånd och konstant spänning.
Också i dessa experiment användes en galvanometer för att mäta strömmen, eftersom spänningenmellan termoelementklämmor proportionell mot anslutningstemperaturen. Han lade sedan till testledningar av olika längder, diametrar och material för att slutföra kretsen. Han fann att hans data kunde modelleras med följande ekvation
x=a /b + l, där x är mätarställningen, l är testledningens längd, a är beroende av temperaturen på termoelementövergången, b är en konstant (konstant) av hela ekvationen. Ohm bevisade sin lag baserat på dessa proportionalitetsberäkningar och publicerade sina resultat.
Vikten av Ohms lag
Ohms lag i differential- och integralform var förmodligen den viktigaste av de tidiga beskrivningarna av elektricitetens fysik. Idag anser vi att detta är nästan självklart, men när Om först publicerade sitt verk var det inte fallet. Kritiker reagerade på hans tolkning med fientlighet. De kallade hans arbete "nakna fantasier" och den tyska utbildningsministern förklarade att "en professor som predikar sådant kätteri är ovärdig att undervisa i vetenskap."
Den rådande vetenskapliga filosofin i Tyskland vid den tiden ansåg att experiment inte var nödvändiga för att utveckla en förståelse av naturen. Dessutom kämpade Geogrs bror, Martin, en matematiker till yrket, med det tyska utbildningssystemet. Dessa faktorer förhindrade acceptansen av Ohms verk, och hans arbete blev inte allmänt accepterat förrän på 1840-talet. Ändå fick Om erkännande för sina bidrag till vetenskapen långt före sin död.
Ohms lag i differential- och integralform är en empirisk lag,generalisering av resultaten från många experiment, som visade att strömmen är ungefär proportionell mot den elektriska fältspänningen för de flesta material. Det är mindre fundament alt än Maxwells ekvationer och är inte lämpligt i alla situationer. Allt material kommer att brytas ner under kraften av ett tillräckligt elektriskt fält.
Ohms lag har observerats på ett brett spektrum av skalor. I början av 1900-talet betraktades inte Ohms lag i atomär skala, men experiment bekräftar motsatsen.
Quantum Beginning
Strömtäthetens beroende av det pålagda elektriska fältet har en fundament alt kvantmekanisk karaktär (klassisk kvantpermeabilitet). En kvalitativ beskrivning av Ohms lag kan baseras på klassisk mekanik med hjälp av Drude-modellen som utvecklades av den tyske fysikern Paul Drude 1900. På grund av detta har Ohms lag många former, såsom den så kallade Ohms lag i differentiell form.
Andra former av Ohms lag
Ohms lag i differentialform är ett extremt viktigt begrepp inom el-/elektronikteknik eftersom den beskriver både spänning och resistans. Allt detta är sammankopplat på makroskopisk nivå. När man studerar elektriska egenskaper på makro- eller mikroskopisk nivå används en mer relaterad ekvation, som kan kallas "Ohms ekvation", med variabler som är nära besläktade med de skalära variablerna V, I och R i Ohms lag, men som är en konstant funktion av position iexplorer.
Effekt av magnetism

Om ett externt magnetfält (B) finns och ledaren inte är i vila, utan rör sig med en hastighet V, måste en extra variabel läggas till för att ta hänsyn till strömmen som induceras av Lorentz-kraften på laddningen transportörer. Kallas även Ohms lag av integralform:
J=σ (E + vB).
I viloramen för en rörlig ledare tas denna term bort eftersom V=0. Det finns inget motstånd eftersom det elektriska fältet i viloramen skiljer sig från E-fältet i laboratorieramen: E'=E + v × B. Elektriska och magnetiska fält är relativa. Om J (ström) är variabel eftersom den applicerade spänningen eller E-fältet varierar med tiden, måste reaktansen läggas till resistansen för att ta hänsyn till självinduktion. Reaktansen kan vara stark om frekvensen är hög eller om ledaren är lindad.






