Varje person under sitt liv möter kroppar som befinner sig i ett av materiens tre aggregerade tillstånd. Det enklaste aggregationstillståndet att studera är gas. I artikeln kommer vi att överväga konceptet med en idealgas, ge systemets tillståndsekvation och även ägna lite uppmärksamhet åt beskrivningen av den absoluta temperaturen.
Gastillstånd
Varje elev har en god uppfattning om vilket tillstånd de talar om när de hör ordet "gas". Detta ord förstås som en kropp som kan uppta vilken volym som helst som den får. Den kan inte behålla sin form, eftersom den inte kan motstå ens den minsta yttre påverkan. Gas behåller inte heller volymen, vilket skiljer den inte bara från fasta ämnen utan också från vätskor.
Som en vätska är en gas ett flytande ämne. I processen för rörelse av fasta kroppar i gaser hindrar de senare denna rörelse. Den resulterande kraften kallas motstånd. Dess värde beror påkroppens hastighet i gasen.
Starka exempel på gaser är luft, naturgas som används för att värma hem och laga mat, inerta gaser (Ne, Ar) som används för att fylla reklamglödrör eller används för att skapa en inert (icke-aggressiv, skyddande) miljö vid svetsning.
Ideal gas
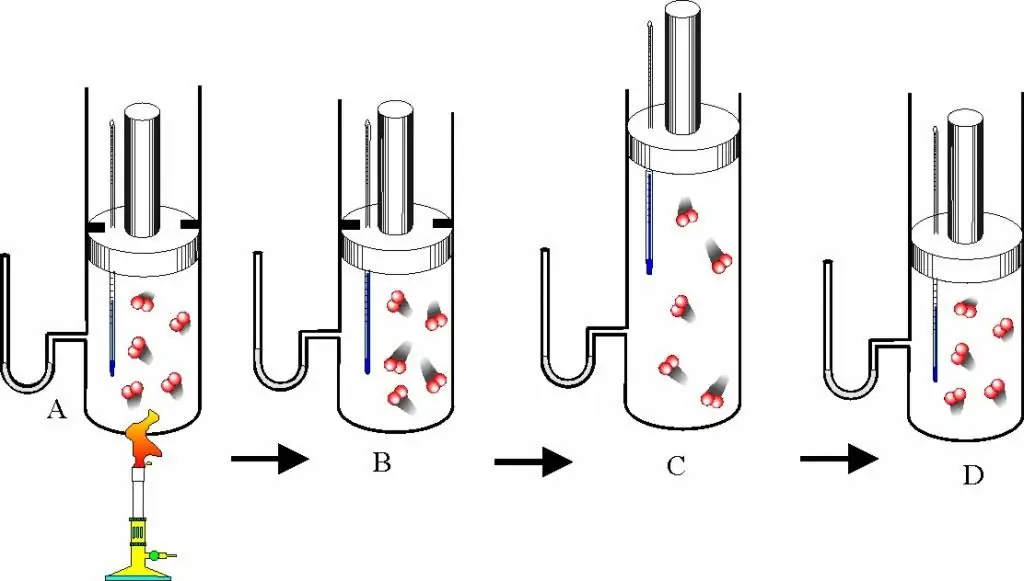
Innan du går vidare till beskrivningen av gaslagar och tillståndsekvationen bör du väl förstå frågan om vad en idealgas är. Detta koncept introduceras i molekylär kinetisk teori (MKT). En idealgas är vilken gas som helst som uppfyller följande egenskaper:
- Partiklarna som bildar den interagerar inte med varandra förutom vid direkta mekaniska kollisioner.
- Som ett resultat av partiklars kollision med kärlets väggar eller sinsemellan bevaras deras kinetiska energi och momentum, det vill säga kollisionen anses vara absolut elastisk.
- Partiklar har inga dimensioner, men har en ändlig massa, det vill säga de liknar materialpunkter.
Det är naturligt att vilken gas som helst inte är idealisk, utan verklig. Ändå, för att lösa många praktiska problem, är dessa approximationer ganska giltiga och kan användas. Det finns en allmän empirisk regel som säger: oavsett den kemiska naturen, om en gas har en temperatur över rumstemperatur och ett tryck i storleksordningen atmosfäriskt eller lägre, så kan den anses vara idealisk med hög noggrannhet och kan användas för att beskriva Det.formeln för den ideala gasekvationen för tillstånd.
Clapeyron-Mendeleev lag
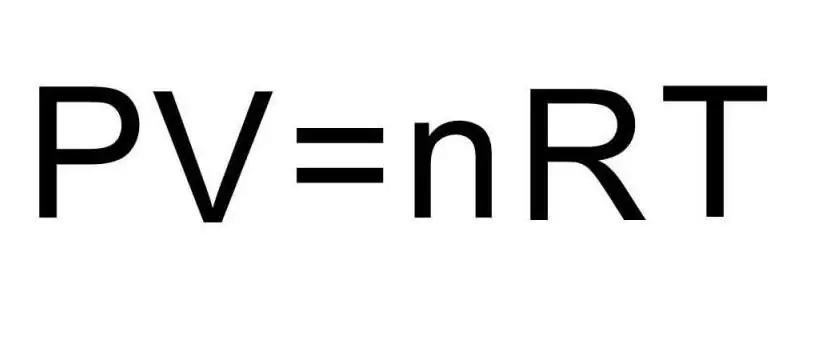
Övergångar mellan olika aggregattillstånd av materia och processer inom ett enda aggregattillstånd hanteras av termodynamik. Tryck, temperatur och volym är tre storheter som unikt definierar varje tillstånd i ett termodynamiskt system. Formeln för tillståndsekvationen för en idealgas kombinerar alla tre av dessa kvantiteter till en enda likhet. Låt oss skriva den här formeln:
PV=nRT
Här P, V, T - tryck, volym, temperatur, respektive. Värdet på n är mängden ämne i mol, och symbolen R betecknar den universella konstanten för gaser. Denna likhet visar att ju större produkten är av tryck och volym, desto större måste produkten vara av mängden ämne och temperatur.

Formeln för tillståndsekvationen för en gas kallas Clapeyron-Mendeleev-lagen. År 1834 kom den franske vetenskapsmannen Emile Clapeyron, som sammanfattade sina föregångares experimentella resultat, till denna ekvation. Clapeyron använde dock ett antal konstanter, som Mendeleev senare ersatte med en - den universella gaskonstanten R (8, 314 J / (molK)). Därför, i modern fysik, är denna ekvation uppkallad efter namnen på franska och ryska forskare.

Andra ekvationsformer
Ovan skrev vi Mendeleev-Clapeyrons tillståndsekvation för en idealisk gas i det allmänt accepterade ochbekväm form. Men vid problem inom termodynamiken kan det ofta krävas en något annan form. Ytterligare tre formler skrivs nedan, som direkt följer av den skrivna ekvationen:
PV=NkBT;
PV=m/MRT;
P=ρRT/M.
Dessa tre ekvationer är också universella för en idealgas, bara i dem förekommer sådana kvantiteter som massa m, molmassa M, densitet ρ och antalet partiklar N som utgör systemet. Symbolen kB här betecknar Boltzmann-konstanten (1, 3810-23J/K).
Boyle-Mariotte Law
När Clapeyron satte upp sin ekvation baserades han på gaslagar som hade upptäckts experimentellt flera decennier tidigare. En av dem är Boyle-Mariotte-lagen. Det återspeglar en isoterm process i ett slutet system, som ett resultat av vilken makroskopiska parametrar som tryck och volym förändras. Om vi sätter T och n konstant i tillståndsekvationen för en idealgas, så kommer gaslagen att ha formen:
P1V1=P2V 2
Detta är Boyle-Mariottes lag, som säger att produkten av tryck och volym bevaras under en godtycklig isoterm process. I det här fallet ändras själva värdena P och V.
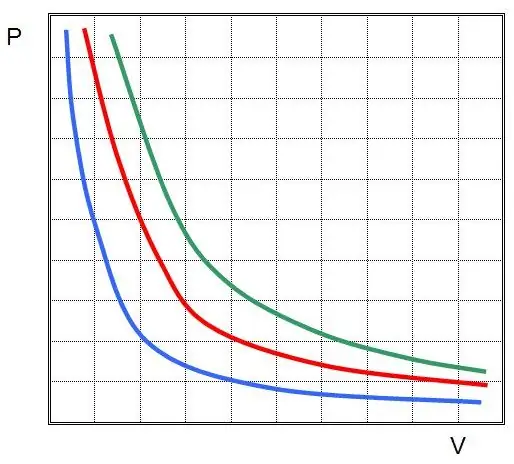
Om du plottar P(V) eller V(P), kommer isotermerna att vara hyperboler.
Charles och Gay-Lussacs lagar
Dessa lagar beskriver matematiskt isobariska och isokoriskaprocesser, det vill säga sådana övergångar mellan gassystemets tillstånd, där tryck respektive volym bevaras. Charles lag kan matematiskt skrivas på följande sätt:
V/T=const när n, P=const.
Gay-Lussacs lag är skriven enligt följande:
P/T=const när n, V=const.
Om båda likheterna presenteras i form av en graf, så får vi raka linjer som lutar i någon vinkel mot x-axeln. Denna typ av graf indikerar en direkt proportionalitet mellan volym och temperatur vid konstant tryck och mellan tryck och temperatur vid konstant volym.
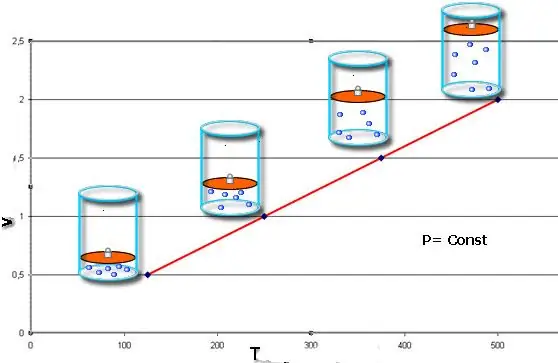
Observera att alla tre övervägda gaslagar inte tar hänsyn till gasens kemiska sammansättning, såväl som förändringen i dess mängd materia.
Absolut temperatur
I vardagen är vi vana vid att använda Celsius-temperaturskalan, eftersom den är bekväm för att beskriva processerna omkring oss. Så vattnet kokar vid 100 oC och fryser vid 0 oC. Inom fysiken visar sig denna skala vara obekväm, därför används den så kallade absoluta temperaturskalan, som introducerades av Lord Kelvin i mitten av 1800-talet. I enlighet med denna skala mäts temperaturen i Kelvin (K).
Man tror att vid en temperatur på -273, 15 oC finns det inga termiska vibrationer av atomer och molekyler, deras framåtrörelse stannar helt. Denna temperatur i grader Celsius motsvarar absolut noll i Kelvin (0 K). Från denna definitionden fysiska betydelsen av absolut temperatur följer: det är ett mått på den kinetiska energin hos de partiklar som utgör materia, till exempel atomer eller molekyler.
Förutom ovanstående fysiska betydelse av absolut temperatur, finns det andra sätt att förstå denna kvantitet. En av dem är den nämnda gaslagen av Charles. Låt oss skriva det i följande form:
V1/T1=V2/T 2=>
V1/V2=T1/T 2.
Den sista likheten säger att vid en viss mängd ämne i systemet (till exempel 1 mol) och ett visst tryck (till exempel 1 Pa), bestämmer gasvolymen unikt den absoluta temperaturen. Med andra ord, en ökning av gasvolymen under dessa förhållanden är möjlig endast på grund av en ökning av temperaturen, och en minskning av volymen indikerar en minskning av värdet på T.
Kom ihåg att, till skillnad från Celsius-temperaturen, kan absolut temperatur inte vara negativ.
Avogadro-principen och gasblandningar
Förutom ovanstående gaslagar, leder tillståndsekvationen för en idealgas också till principen som upptäcktes av Amedeo Avogadro i början av 1800-talet och som bär hans efternamn. Denna princip fastställer att volymen av en gas vid konstant tryck och temperatur bestäms av mängden ämne i systemet. Motsvarande formel ser ut så här:
n/V=const när P, T=const.
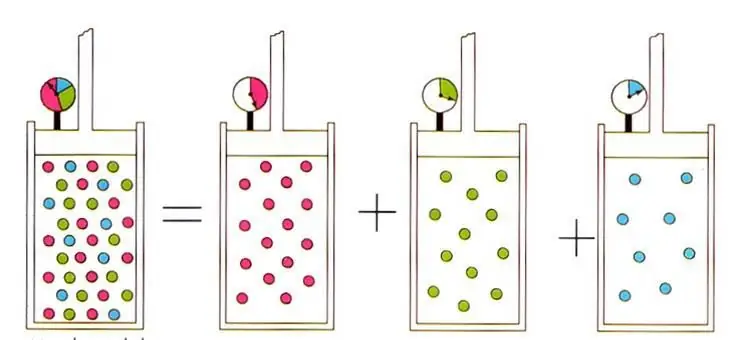
Det skriftliga uttrycket leder till den inom idealgasfysiken välkända D altons lag för gasblandningar. Dettalagen säger att parti altrycket för en gas i en blandning bestäms unikt av dess atomfraktion.
Exempel på problemlösning
I ett slutet kärl med styva väggar som innehåller en idealisk gas ökade trycket tre gånger till följd av uppvärmning. Det är nödvändigt att bestämma systemets sluttemperatur om dess initiala värde var 25 oC.
Först, låt oss konvertera temperaturen från grader Celsius till Kelvin, vi har:
T=25 + 273, 15=298, 15 K.
Eftersom kärlets väggar är stela kan uppvärmningsprocessen betraktas som isokorisk. I det här fallet tillämpar vi Gay-Lussac-lagen, vi har:
P1/T1=P2/T 2=>
T2=P2/P1T 1.
Därmed bestäms sluttemperaturen från produkten av tryckförhållandet och initi altemperaturen. Genom att ersätta data med jämlikhet får vi svaret: T2=894,45 K. Denna temperatur motsvarar 621,3 oC.






