Termodynamik för materiens gasformiga aggregattillstånd är en viktig gren av fysiken som studerar termodynamisk jämvikt och kvasistatiska övergångar i system. Den huvudsakliga modellen som förutsägelser av systemens beteende bygger på är den ideala gasmodellen. Med dess användning erhölls Mendeleev-Clapeyron-ekvationen. Tänk på det i artikeln.
Ideal gas
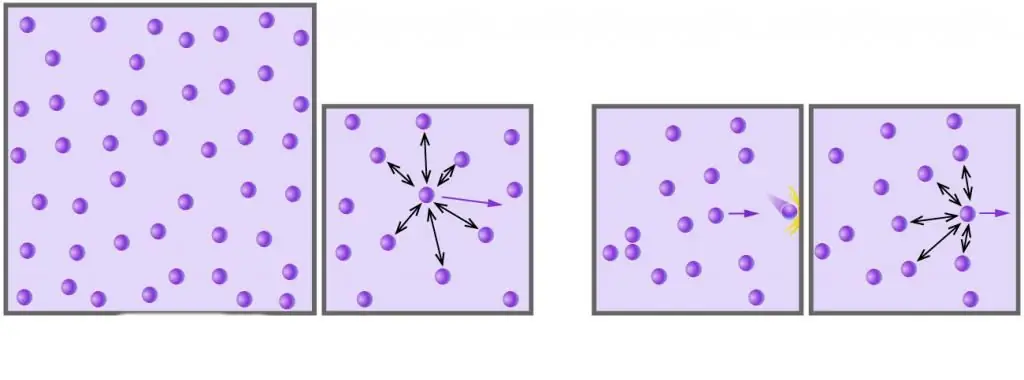
Som ni vet består alla verkliga gaser av molekyler eller atomer, vars avstånd är för stora jämfört med deras storlek vid låga tryck. Dessutom, vid höga temperaturer, i en absolut skala, överstiger den kinetiska energin hos molekyler deras potentiella energi förknippad med svaga dipol-dipol-interaktioner (om det, förutom dessa interaktioner, finns andra typer av kemiska bindningar, till exempel jon- eller väte, då ger de ett betydande bidrag till den potentiella komponenten i den interna systemets energi).
På grund avFör många riktiga gaser under förhållanden nära normala kan man försumma deras interna interaktioner och partikelstorlekar. Dessa två huvudsakliga uppskattningar utgör den ideala gasmodellen.
Mendeleevs ekvation i fysik

Det är mer korrekt och rättvist att kalla denna ekvation för Clapeyron-Mendeleev-lagen. Faktum är att det först spelades in av den franske ingenjören Emile Clapeyron 1834. Han gjorde detta genom att analysera gaslagarna för Boyle-Mariotte, Gay-Lussac och Charles som upptäcktes i början av 1800-talet.
Den ryske kemisten Dmitrij Mendeleevs förtjänst ligger i det faktum att han gav ekvationen en modern och lättanvänd matematisk form. I synnerhet införde Mendeleev i ekvationen en konstant för alla gaser R=8, 314 J/(molK). Clapeyron själv använde ett antal empiriska konstanter som gör beräkningsprocessen svår.
Mendeleev-Clapeyrons ekvation skrivs enligt följande:
PV=nRT.
Denna likhet innebär att produkten av trycket P och volymen V på vänster sida av uttrycket alltid är proportionell mot produkten av absolut temperatur T och mängden ämne n på vänster sida.
Uttrycket som studeras låter dig få vilken gaslag som helst om du fixar två av dess fyra parametrar. När det gäller isoprocesser studeras slutna system där det inte sker något utbyte av materia med omgivningen (n=const). Dessa processer kännetecknas av en enda fast termodynamisk parameter (T, P eller V).

Exempelproblem
Låt oss nu lösa problemet med Mendeleev-Clapeyron-ekvationen. Det är känt att syre som väger 500 gram finns i en cylinder med en volym på 100 liter vid ett tryck av 2 atmosfärer. Vad är temperaturen i ballongen, givet att systemet är i termodynamisk jämvikt.
Kom ihåg att mängden av ett ämne enligt definitionen beräknas med formeln:
n=m/M.
Där m är massan av alla partiklar i systemet, är M deras genomsnittliga molmassa. Denna likhet gör det möjligt för oss att skriva om Mendelejevs ekvation i följande form:
PV=mRT/M.
Var vi får arbetsformeln för denna uppgift:
T=PVM/(mR).
Det återstår att konvertera alla kvantiteter till SI-enheter och ersätta dem med detta uttryck:
T=21013250, 10, 032/(0, 58, 314)=156 K.
Beräknad temperatur är -117 oC. Även om syre vid denna temperatur fortfarande är gasformigt (det kondenserar vid -182,96 oC), kan den ideala gasmodellen under sådana förhållanden endast användas för att erhålla en kvalitativ uppskattning av det beräknade värdet.






