Att studera egenskaperna hos en idealgas är ett viktigt ämne inom fysiken. Introduktion till egenskaperna hos gassystem börjar med en övervägande av Boyle-Mariottes ekvation, eftersom det är den första experimentellt upptäckta lagen för en idealgas. Låt oss överväga det mer i detalj i artikeln.
Vad menas med en idealisk gas?
Innan vi pratar om Boyle-Mariottes lag och ekvationen som beskriver den, låt oss definiera en idealisk gas. Det är allmänt uppfattat som ett flytande ämne där partiklarna som utgör det inte interagerar med varandra, och deras storlekar är försumbart små i jämförelse med de genomsnittliga avstånden mellan partiklarna.
Faktum är att vilken gas som helst är verklig, det vill säga dess ingående atomer och molekyler har en viss storlek och interagerar inte med varandra med hjälp av van der Waals-krafter. Men vid höga absoluta temperaturer (mer än 300 K) och låga tryck (mindre än en atmosfär) är den kinetiska energin för atomer och molekyler mycket högre än energin för van der Waals interaktioner, så den verkliga gasen vid den angivnaförhållanden med hög noggrannhet kan anses vara idealiska.
Boyle-Mariottes ekvation
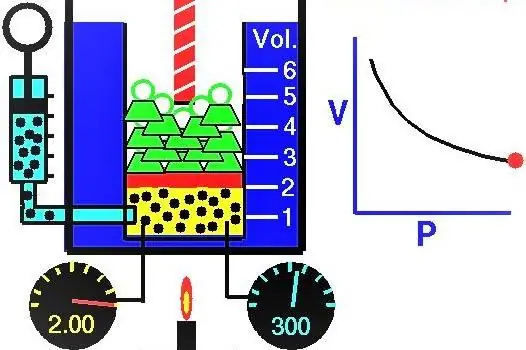
Egenskaper hos gaser Europeiska vetenskapsmän utforskade aktivt under XVII-XIX århundradena. Den allra första gaslagen som upptäcktes experimentellt var lagen som beskrev de isotermiska processerna för expansion och kompression av ett gassystem. Motsvarande experiment utfördes av Robert Boyle 1662 och Edm Mariotte 1676. Var och en av dessa forskare visade oberoende att under en isotermisk process i ett slutet gassystem ändras trycket omvänt med volymen. Det experimentellt erhållna matematiska uttrycket för processen skrivs i följande form:
PV=k
Där P och V är trycket i systemet och dess volym, är k någon konstant, vars värde beror på mängden gasämne och dess temperatur. Om du bygger beroendet av P(V)-funktionen på en graf, så blir det en hyperbel. Ett exempel på dessa kurvor visas nedan.
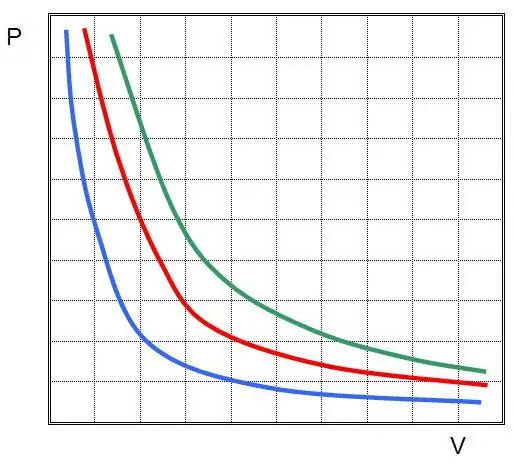
Den skriftliga likheten kallas Boyle-Mariottes ekvation (lag). Denna lag kan kort formuleras enligt följande: expansionen av en idealgas vid en konstant temperatur leder till en proportionell minskning av trycket i den, tvärtom åtföljs isotermisk kompression av ett gassystem av en proportionell ökning av trycket i det.
Den idealiska gasekvationen
Boyle-Mariottes lag är ett specialfall av en mer allmän lag som bär namnen Mendeleev ochClapeyron. Emile Clapeyron, som sammanfattar den experimentella informationen om gasernas beteende under olika yttre förhållanden, erhöll 1834 följande ekvation:
PV=nRT
Med andra ord, produkten av volymen V i ett gassystem och trycket P i det är direkt proportionell mot produkten av den absoluta temperaturen T och mängden ämne n. Koefficienten för denna proportionalitet betecknas med bokstaven R och kallas gasens universella konstant. I den skrivna ekvationen dök värdet på R upp på grund av utbytet av ett antal konstanter, som gjordes av Dmitrij Ivanovitj Mendelejev 1874.
Från den universella tillståndsekvationen är det lätt att se att temperaturens konstantitet och mängden substans garanterar invariansen av den högra sidan av ekvationen, vilket innebär att den vänstra sidan av ekvationen också kommer att förbli konstant. I det här fallet får vi Boyle-Mariottes ekvation.

Andra gaslagar
Clapeyron-Mendeleev-ekvationen som skrivits i stycket ovan innehåller tre termodynamiska parametrar: P, V och T. Om var och en av dem är fixerade, och de andra två tillåts ändras, får vi Boyle-Mariotte, Charles och Gay-Lussacs ekvationer. Charles lag talar om en direkt proportionalitet mellan volym och temperatur för en isobar process, och Gay-Lussacs lag säger att vid en isokorisk övergång ökar eller minskar gastrycket i direkt proportion till den absoluta temperaturen. Motsvarande ekvationer ser ut så här:
V/T=const när P=const;
P/T=const när V=const.
SåBoyle-Mariottes lag är alltså en av de tre huvudsakliga gaslagarna. Den skiljer sig dock från resten när det gäller grafiskt beroende: funktionerna V(T) och P(T) är räta linjer, funktionen P(V) är en hyperbel.
Exempel på en uppgift för tillämpning av Boyle-Mariotte-lagen
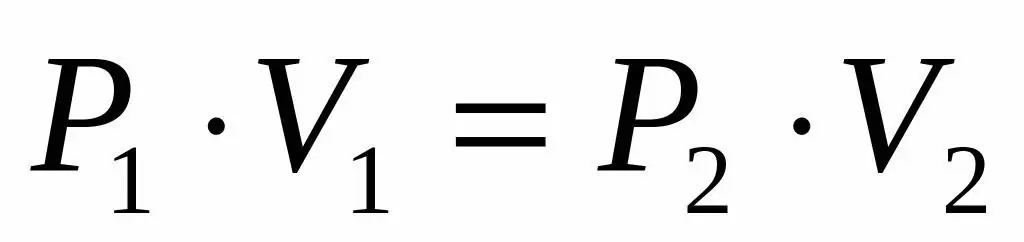
Volymen gas i cylindern under kolven i utgångsläget var 2 liter och dess tryck var 1 atmosfär. Vad var trycket på gasen efter att kolven steg och gassystemets volym ökade med 0,5 liter. Processen anses vara isotermisk.
Eftersom vi får trycket och volymen för en idealgas, och vi också vet att temperaturen förblir oförändrad under dess expansion, kan vi använda Boyle-Mariottes ekvation i följande form:
P1V1=P2V 2
Denna likhet säger att volym-tryck-produkten är konstant för varje tillstånd av gasen vid en given temperatur. Genom att uttrycka värdet P2 från likhet, får vi den slutliga formeln:
P2=P1V1/V 2
När du gör tryckberäkningar kan du använda enheter utanför systemet i det här fallet, eftersom liter kommer att krympa och vi får trycket P2i atmosfärer. Genom att ersätta data från villkoret kommer vi fram till svaret på frågan om problemet: P2=0,8 atmosfärer.






