Idealgas, den ideala gasekvationen för tillstånd, dess temperatur och tryck, volym… listan över parametrar och definitioner som används i motsvarande sektion av fysiken kan fortsätta under ganska lång tid. Idag ska vi bara prata om detta ämne.
Vad betraktas i molekylär fysik?

Huvudobjektet som tas upp i detta avsnitt är en idealisk gas. Den ideala gasekvationen för tillstånd erhölls med hänsyn till normala miljöförhållanden, och vi kommer att prata om detta lite senare. Låt oss nu närma oss detta "problem" på långt håll.
Låt oss säga att vi har en massa gas. Dess tillstånd kan bestämmas med hjälp av tre parametrar av termodynamisk natur. Dessa är naturligtvis tryck, volym och temperatur. Ekvationen för systemets tillstånd i detta fall kommer att vara formeln för förhållandet mellan motsvarande parametrar. Det ser ut så här: F (p, V, T)=0.
Här, för första gången, närmar vi oss sakta framväxten av något sådant som idealgas. Det kallas en gas där interaktionerna mellan molekyler är försumbara. I allmänhet finns detta inte i naturen. Men all mycket förtärnad gas är nära den. Kväve, syre och luft, som är under normala förhållanden, skiljer sig lite från det ideala. För att skriva tillståndsekvationen för en idealgas kan vi använda den förenade gaslagen. Vi får: pV/T=const.
Relaterat koncept 1: Avogadros lag
Han kan berätta för oss att om vi tar samma antal mol av absolut vilken slumpmässig gas som helst och sätter dem under samma förhållanden, inklusive temperatur och tryck, så kommer gaserna att uppta samma volym. I synnerhet utfördes experimentet under normala förhållanden. Det betyder att temperaturen var 273,15 Kelvin, trycket var en atmosfär (760 millimeter kvicksilver, eller 101325 Pascal). Med dessa parametrar upptog gasen en volym lika med 22,4 liter. Därför kan vi säga att för en mol av vilken gas som helst kommer förhållandet mellan numeriska parametrar att vara ett konstant värde. Det är därför man beslutade att beteckna denna siffra med bokstaven R och kalla den den universella gaskonstanten. Det är alltså lika med 8,31. Enheten är J/molK.
Ideal gas. Den ideala gasekvationen för tillstånd och dess manipulation
Låt oss försöka skriva om formeln. För att göra detta skriver vi det i denna form: pV=RT. Därefter utför vi en enkel handling, multiplicerar båda sidor av ekvationen med ett godtyckligt antal mol. Vi får pVu=uRT. Låt oss ta hänsyn till det faktum att produkten av molvolymen ochmängden materia är helt enkelt volymen. Men trots allt kommer antalet mol samtidigt att vara lika med kvoten av massan och molmassan. Det är precis så här Mendeleev-Clapeyrons ekvation ser ut. Det ger en tydlig uppfattning om vilken typ av system en idealgas bildas. Tillståndsekvationen för en idealgas kommer att ha formen: pV=mRT/M.
Härleda formeln för tryck
Låt oss göra några fler manipulationer med de erhållna uttrycken. För att göra detta multipliceras den högra sidan av Mendeleev-Clapeyrons ekvation och divideras med Avogadro-talet. Nu tittar vi noggrant på produkten av mängden ämne med Avogadro-talet. Detta är inget annat än det totala antalet molekyler i gasen. Men samtidigt kommer förhållandet mellan den universella gaskonstanten och Avogadro-talet att vara lika med Boltzmann-konstanten. Därför kan formler för tryck skrivas på följande sätt: p=NkT/V eller p=nkT. Här är symbolen n partikelkoncentrationen.
Ideala gasprocesser
Inom molekylär fysik finns det något sådant som isoprocesser. Dessa är termodynamiska processer som äger rum i systemet vid en av de konstanta parametrarna. I det här fallet måste även ämnets massa förbli konstant. Låt oss titta på dem mer specifikt. Så, lagarna för en ideal gas.
Trycket förblir konstant
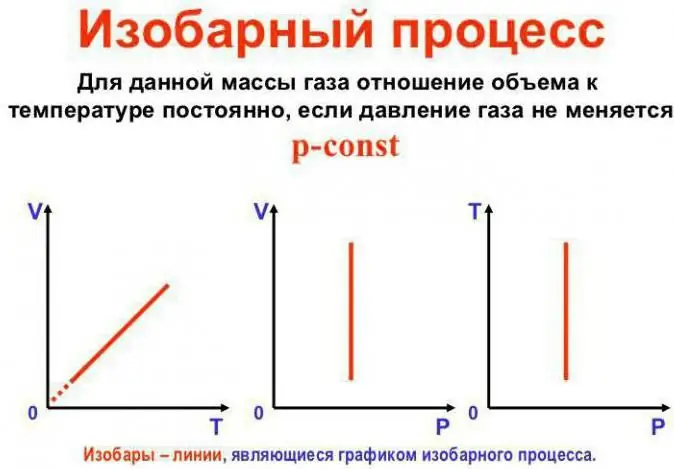
Detta är Gay-Lussacs lag. Det ser ut så här: V/T=konst. Det kan skrivas om på ett annat sätt: V=Vo (1 + at). Här är a lika med 1/273,15 K^-1 och kallas "volymexpansionskoefficienten". Vi kan ersätta temperaturen i både Celsius ochKelvinskalan. I det senare fallet får vi formeln V=Voat.
Volymen förblir konstant

Detta är Gay-Lussacs andra lag, mer allmänt kallad Charles' lag. Det ser ut så här: p/T=konst. Det finns en annan formulering: p=po (1 + at). Transformationer kan utföras i enlighet med föregående exempel. Som du kan se är de ideala gaslagarna ibland ganska lika varandra.
Temperaturen förblir konstant

Om temperaturen på en idealgas förblir konstant, kan vi få Boyle-Mariottes lag. Det kan skrivas så här: pV=const.
Relaterat koncept 2: partiellt tryck
Låt oss säga att vi har ett fartyg med gaser. Det blir en blandning. Systemet befinner sig i ett tillstånd av termisk jämvikt och själva gaserna reagerar inte med varandra. Här kommer N att beteckna det totala antalet molekyler. N1, N2 och så vidare, respektive antalet molekyler i var och en av komponenterna i blandningen. Låt oss ta tryckformeln p=nkT=NkT/V. Den kan öppnas för ett specifikt fall. För en tvåkomponentsblandning kommer formeln att ha formen: p=(N1 + N2) kT/V. Men sedan visar det sig att det totala trycket kommer att summeras från parti altrycken för varje blandning. Så det kommer att se ut som p1 + p2 och så vidare. Dessa kommer att vara deltrycken.
Vad är det till för?
Formeln vi fick anger att trycket i systemet kommer från varje grupp av molekyler. Det beror för övrigt inte påandra. D alton drog fördel av detta när han formulerade lagen, senare uppkallad efter honom: i en blandning där gaser inte reagerar kemiskt med varandra kommer det totala trycket att vara lika med summan av parti altrycken.






