Elasticitetsmodul är en fysisk storhet som kännetecknar det elastiska beteendet hos ett material när en yttre kraft appliceras på det i en viss riktning. Det elastiska beteendet hos ett material betyder dess deformation i det elastiska området.
Historia om studiet av elasticitet hos material

Den fysiska teorin om elastiska kroppar och deras beteende under inverkan av yttre krafter övervägdes i detalj och studerades av den engelska vetenskapsmannen på 1800-talet, Thomas Young. Men själva begreppet elasticitet utvecklades redan 1727 av den schweiziske matematikern, fysikern och filosofen Leonhard Euler, och de första experimenten relaterade till elasticitetsmodulen utfördes 1782, det vill säga 25 år före Thomas Jungs arbete., av den venetianske matematikern och filosofen Jacopo Ricatti.
Thomas Youngs förtjänst ligger i det faktum att han gav elasticitetsteorin ett slankt modernt utseende, som sedan formaliserades i form av en enkel och sedan generaliserad Hookes lag.
Elasticitetens fysiska karaktär
Varje kropp som helst består av atomer, mellan vilka attraktions- och repulsionskrafterna verkar. Balansen mellan dessa krafter ärmateriens tillstånd och parametrar under givna förhållanden. Atomerna i en fast kropp, när obetydliga yttre spännings- eller kompressionskrafter appliceras på dem, börjar förskjutas, vilket skapar en kraft i motsatt riktning och lika stor, som tenderar att återföra atomerna till deras ursprungliga tillstånd.
I processen med sådan förskjutning av atomer ökar energin i hela systemet. Experiment visar att vid små stammar är energin proportionell mot kvadraten av dessa stammar. Detta betyder att kraften, som är en derivata med avseende på energi, visar sig vara proportionell mot töjningens första potens, det vill säga den beror linjärt på den. Genom att svara på frågan, vad är elasticitetsmodulen, kan vi säga att detta är proportionalitetskoefficienten mellan kraften som verkar på atomen och deformationen som denna kraft orsakar. Dimensionen på Youngs modul är densamma som dimensionen för trycket (Pascal).
Elastisk gräns
Enligt definitionen indikerar elasticitetsmodulen hur mycket spänning som måste anbringas på ett fast ämne för att dess deformation ska vara 100 %. Alla fasta ämnen har dock en elasticitetsgräns lika med 1 % töjning. Detta betyder att om en lämplig kraft appliceras och kroppen deformeras med en mängd mindre än 1%, så återställer kroppen exakt sin ursprungliga form och dimensioner efter att denna kraft har upphört. Om för mycket kraft appliceras, vid vilken deformationsvärdet överstiger 1%, kommer kroppen inte längre att återställa sina ursprungliga dimensioner efter att den yttre kraften har avslutats. I det senare fallet talar man om förekomsten av en restdeformation, dvsbevis på att materialets elasticitetsgräns har överskridits.
Youngs modul i aktion
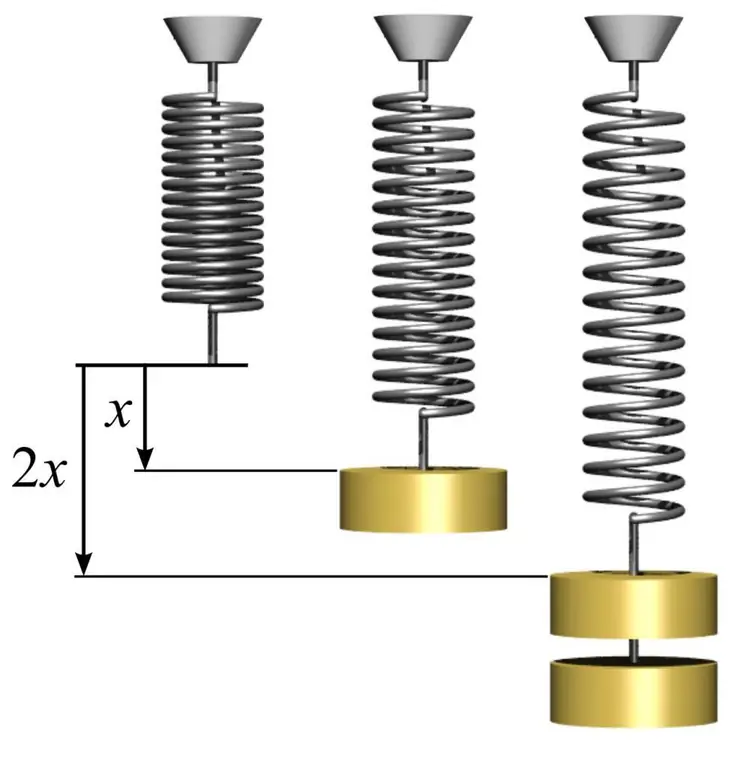
För att bestämma elasticitetsmodulen, samt för att förstå hur man använder den, kan du ge ett enkelt exempel med en fjäder. För att göra detta måste du ta en metallfjäder och mäta arean av cirkeln som dess spolar bildar. Detta görs med den enkla formeln S=πr², där n är pi lika med 3,14 och r är radien på fjäderns spole.
Nästa, mät längden på fjädern l0 utan belastning. Om du hänger någon last med massa m1 på en fjäder, kommer den att öka sin längd till ett visst värde l1. Elasticitetsmodulen E kan beräknas baserat på kunskapen om Hookes lag med formeln: E=m1gl0/(S(l) 1-l0)), där g är accelerationen för fritt fall. I det här fallet noterar vi att mängden deformation av fjädern i det elastiska området kan avsevärt överstiga 1%.
Genom att känna till Youngs modul kan du förutsäga mängden deformation under inverkan av en viss stress. I det här fallet, om vi hänger en annan massa m2 på fjädern, får vi följande värde på relativ deformation: d=m2g/ (SE), där d - relativ deformation i det elastiska området.
Isotropi och anisotropi
Elasticitetsmodul är en egenskap hos ett material som beskriver styrkan hos bindningen mellan dess atomer och molekyler, men ett visst material kan ha flera olika Youngs moduler.
Faktum är att egenskaperna hos varje fast ämne beror på dess inre struktur. Om egenskaperna är desamma i alla rumsliga riktningar, då talar vi om ett isotropiskt material. Sådana ämnen har en homogen struktur, så verkan av en yttre kraft i olika riktningar på dem orsakar samma reaktion från materialet. Alla amorfa material är isotropa, som gummi eller glas.
Anisotropi är ett fenomen som kännetecknas av att de fysikaliska egenskaperna hos en fast eller vätska är beroende av riktning. Alla metaller och legeringar baserade på dem har ett eller annat kristallgitter, det vill säga ett ordnat snarare än ett kaotiskt arrangemang av joniska kärnor. För sådana material varierar elasticitetsmodulen beroende på verkansaxeln för den yttre spänningen. Till exempel har metaller med kubisk symmetri, såsom aluminium, koppar, silver, eldfasta metaller och andra, tre olika Youngs moduler.
Skärningsmodul
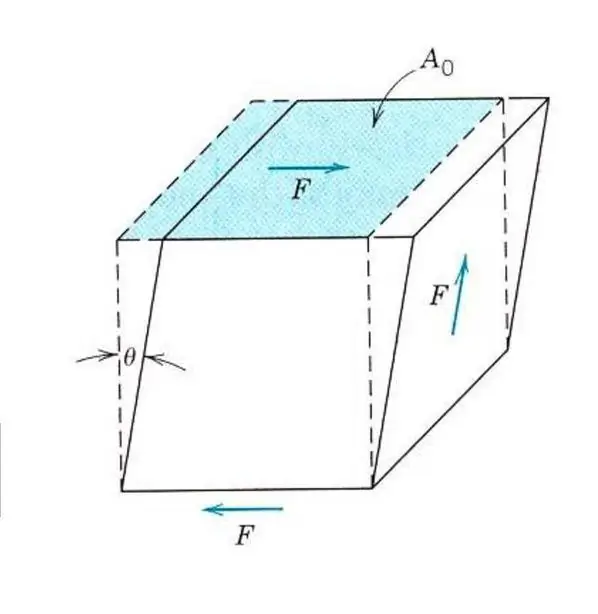
Beskrivning av de elastiska egenskaperna hos även ett isotropiskt material kräver inte kunskap om en Youngs modul. Eftersom materialet, förutom spänning och kompression, kan påverkas av skjuvspänningar eller vridspänningar. I det här fallet kommer den att reagera annorlunda på yttre kraft. För att beskriva elastisk skjuvdeformation introduceras en analog av Youngs modul, skjuvmodul eller elasticitetsmodul av det andra slaget.
Alla material motstår skjuvspänningar som är mindre än spänning eller kompression, så skjuvmodulvärdet för dem är 2-3 gånger mindre än värdet för Youngs modul. Således, för titan, vars Youngs modul är lika med 107 GPa, är skjuvmodulenendast 40 GPa, för stål är dessa siffror 210 GPa respektive 80 GPa.
Elasticitetsmodul för trä

Trä är ett anisotropiskt material eftersom träfibrer är orienterade i en specifik riktning. Det är längs fibrerna som träets elasticitetsmodul mäts, eftersom den är 1-2 storleksordningar mindre över fibrerna. Kunskap om Youngs modul för trä är viktig och beaktas vid design av träpanelstrukturer.
Värdena för träets elasticitetsmodul för vissa typer av träd visas i tabellen nedan.
| Trädvy | Youngs modul i GPa |
| Laurel tree | 14 |
| Eucalyptus | 18 |
| Cedar | 8 |
| Spruce | 11 |
| Pine | 10 |
| Ek | 12 |
Det bör noteras att de angivna värdena kan skilja sig med upp till 1 GPa för ett visst träd, eftersom dess Youngs modul påverkas av träets densitet och växtförhållanden.

Skärningsmoduler för olika trädslag ligger i intervallet 1-2 GPa, till exempel för tall är det 1,21 GPa och för ek 1,38 GPa, det vill säga trä motstår praktiskt taget inte skjuvpåkänningar. Detta faktum måste beaktas vid tillverkning av bärande träkonstruktioner, som är konstruerade för att endast fungera i spänning eller kompression.
Elastiska egenskaper hos metaller
Jämfört med Youngs modul för trä, är medelvärdena för detta värde för metaller och legeringar en storleksordning större, som visas i följande tabell.
| Metal | Youngs modul i GPa |
| Brons | 120 |
| Copper | 110 |
| Stål | 210 |
| Titanium | 107 |
| Nickel | 204 |
Elastiska egenskaper hos metaller som har en kubisk syngoni beskrivs av tre elastiska konstanter. Sådana metaller inkluderar koppar, nickel, aluminium, järn. Om en metall har en hexagonal syngoni, behövs redan sex konstanter för att beskriva dess elastiska egenskaper.
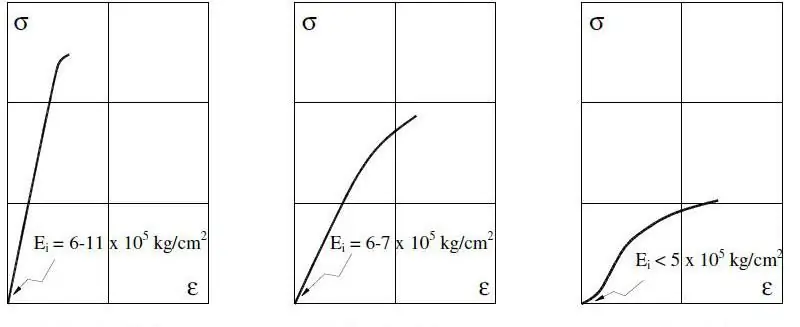
För metalliska system mäts Youngs modul inom 0,2 % töjning, eftersom stora värden redan kan förekomma i det oelastiska området.






