I fysiken studeras ämnet parallell- och seriekoppling, och det kan inte bara vara ledare utan även kondensatorer. Det är viktigt här att inte bli förvirrad över hur var och en av dem ser ut på diagrammet. Och först då tillämpa specifika formler. Förresten, du måste komma ihåg dem utantill.
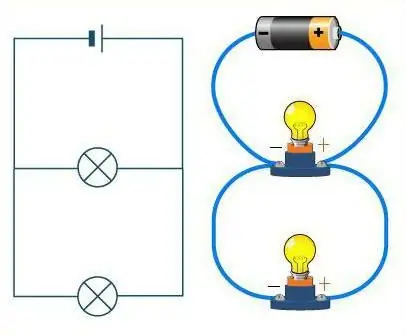
Hur skiljer man mellan dessa två föreningar?
Ta en närmare titt på diagrammet. Om ledningarna representeras som en väg, kommer bilarna på den att spela rollen som motstånd. På en rak väg utan gafflar kör bilar efter varandra, i en kedja. Seriekopplingen av ledare ser också likadan ut. Vägen i det här fallet kan ha ett obegränsat antal svängar, men inte en enda korsning. Oavsett hur vägen (trådarna) viftade, kommer maskinerna (motstånden) alltid att vara placerade efter varandra, i en kedja.
Det är en helt annan sak om en parallellkoppling övervägs. Då kan motstånden jämföras med idrottare i starten. Dom ärvar och en står på sitt eget spår, men de har samma rörelseriktning, och mållinjen är på samma plats. På samma sätt, motstånd - var och en av dem har sin egen tråd, men de är alla anslutna någon gång.
Formler för nuvarande styrka
Det diskuteras alltid i ämnet "El". Parallell- och seriekopplingar påverkar mängden ström i motstånd på olika sätt. För dem härleds formler som kan kommas ihåg. Men det räcker med att komma ihåg betydelsen som investeras i dem.
Så, strömmen i seriekoppling av ledare är alltid densamma. Det vill säga, i var och en av dem är värdet på den nuvarande styrkan inte annorlunda. Du kan dra en analogi om du jämför en tråd med ett rör. I den rinner alltid vatten på samma sätt. Och alla hinder på dess väg kommer att sopas bort med samma kraft. Samma med nuvarande. Därför ser formeln för den totala strömmen i en krets med seriekoppling av motstånd ut så här:
I gen=I 1=I 2
Här betecknar bokstaven I strömstyrkan. Detta är en vanlig notation, så du måste komma ihåg den.
Strömmen i parallellkoppling kommer inte längre att vara ett konstant värde. Med samma analogi med ett rör visar det sig att vattnet kommer att delas i två bäckar om huvudröret har en gren. Samma fenomen observeras med ström när en förgrening av ledningar dyker upp i dess väg. Formeln för den totala strömstyrkan när ledarna är parallellkopplade:
I gen=I 1 + I 2
Om förgreningen består av ledningar sommer än två, då kommer det i formeln ovan att finnas fler termer med samma nummer.
Formler för stress
När en krets betraktas där ledarna är seriekopplade, bestäms spänningen i hela sektionen av summan av dessa värden på varje specifikt motstånd. Du kan jämföra denna situation med tallrikar. Det kommer att vara lätt för en person att hålla i en av dem, han kommer också att kunna ta den andra i närheten, men med svårighet. En person kommer inte längre att kunna hålla tre tallrikar bredvid varandra, hjälp av en andra kommer att krävas. Etc. Människors ansträngningar går ihop.
Formeln för den totala spänningen för en sektion av en krets med seriekoppling av ledare ser ut så här:
U gen=U 1 + U 2, där U är den antagna beteckningen för elektrisk spänning.
En annan situation uppstår om en parallellkoppling av motstånd övervägs. När tallrikar staplas ovanpå varandra kan de fortfarande hållas av en person. Så du behöver inte lägga till något. Samma analogi observeras när ledarna är parallellkopplade. Spänningen på var och en av dem är densamma och lika med den som finns på dem alla samtidigt. Formeln för total spänning är:
U gen=U 1=U 2
Formler för elektriskt motstånd
Du kan inte längre memorera dem, men kan formeln för Ohms lag och härleda den önskade från den. Av denna lag följer attspänningen är lika med produkten av ström och resistans. Det vill säga U=IR, där R är motståndet.
Då beror formeln du kommer att behöva arbeta med på hur ledarna är anslutna:
- i serie, så du behöver likvärdighet för spänning - IgenRtotal=I1R1 + I2R2;
- parallellt är det nödvändigt att använda formeln för strömstyrkan - Utotal / Rtotal=U 1/ R1 + U2 / R2 .
Följt av enkla transformationer, som bygger på det faktum att i den första likheten har alla strömmar samma värde, och i den andra - spänningarna är lika. Så de kan förkortas. Det vill säga följande uttryck erhålls:
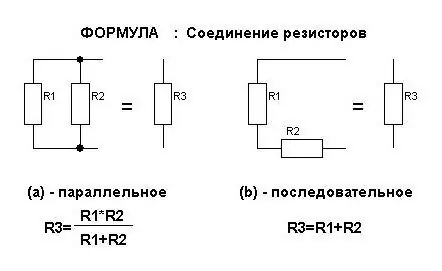
- R gen=R 1 + R 2 (för seriekoppling av ledare)
- 1 / R gen=1 / R 1 + 1 / R 2(vid parallellkopplad).
När antalet motstånd som är anslutna till nätverket ökar, ändras antalet termer i dessa uttryck.
Det är värt att notera att parallell- och seriekoppling av ledare har olika effekt på det totala motståndet. Den första av dem minskar motståndet i kretssektionen. Dessutom visar det sig vara mindre än den minsta av de använda motstånden. När det är seriekopplat är allt logiskt: värdena läggs ihop, så det totala antalet kommer alltid att vara störst.
Arbetsaktuellt
De tre föregående storheterna utgör lagarna för parallellkoppling och seriearrangemang av ledare i en krets. Därför är det absolut nödvändigt att känna till dem. Om arbete och makt behöver du bara komma ihåg den grundläggande formeln. Det är skrivet som följer: A \u003d IUt, där A är strömmens verk, t är tiden för dess passage genom ledaren.
För att bestämma det totala arbetet med en seriell anslutning måste du byta ut spänningen i det ursprungliga uttrycket. Du får likheten: A \u003d I(U 1 + U 2)t, öppna parentesen där det visar sig att arbete på hela avsnittet är lika med beloppet för varje specifik aktuell konsument.
Resonemangen fortsätter på liknande sätt om ett parallellkopplingsschema övervägs. Endast den nuvarande styrkan är tänkt att bytas ut. Men resultatet blir detsamma: A=A 1 + A 2.
Aktuell effekt
När du härleder en formel för effekt (notation "P") för en kretssektion, måste du återigen använda en formel: P \u003d UI. Efter ett sådant resonemang visar det sig att parallell- och seriekopplingar är beskrivs av en sådan formel för makt: P \u003d P1 + P 2.
Det vill säga, oavsett hur scheman utformas så kommer den totala kraften att vara summan av de som är involverade i arbetet. Detta förklarar det faktum att det är omöjligt att inkludera många kraftfulla enheter i lägenhetsnätverket samtidigt. Hon orkar helt enkelt inte.
Hur påverkar anslutningen av ledare reparationen av nyårsgirlangen?
Omedelbart efter att en av glödlamporna brinner ut står det klart hur de kopplades ihop. Påseriell anslutning, kommer ingen av dem att lysa. Detta beror på att en lampa som blivit oanvändbar skapar ett avbrott i kretsen. Därför måste du kontrollera allt för att avgöra vilken som är utbränd, byt ut den - och kransen börjar fungera.
Om den använder en parallellanslutning, slutar den inte fungera om en av glödlamporna går sönder. När allt kommer omkring kommer kedjan inte att brytas helt, utan bara en parallell del. För att reparera en sådan krans behöver du inte kontrollera alla element i kretsen, utan bara de som inte lyser.
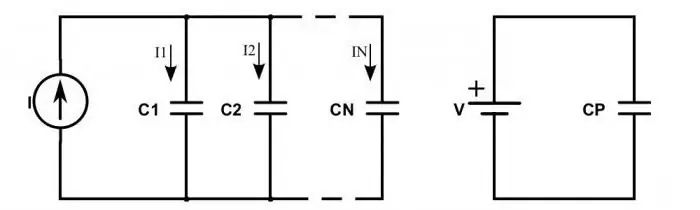
Vad händer med en krets om kondensatorer ingår istället för motstånd?
När de är seriekopplade observeras följande situation: laddningar från strömkällans plusser kommer endast till de yttre plattorna på de extrema kondensatorerna. De där emellan skickar helt enkelt den laddningen längs kedjan. Detta förklarar det faktum att samma laddningar förekommer på alla tallrikar, men med olika tecken. Därför kan den elektriska laddningen för varje seriekopplad kondensator skrivas enligt följande:
q gen =q 1=q 2.
För att bestämma spänningen på varje kondensator måste du känna till formeln: U=q / C. I den är C kondensatorns kapacitans.
Total spänning följer samma lag som motstånd. Genom att ersätta spänningen i kapacitansformeln med summan får vi därför att den totala kapacitansen för enheterna måste beräknas med formeln:
C=q / (U 1 + U2).
Du kan förenkla den här formeln genom att vända på bråken och ersätta förhållandet mellan spänning och laddning med kapacitans. Det visar sig följande likhet: 1 / С=1 / С 1 + 1 / С 2.
Situationen ser något annorlunda ut när kondensatorerna är parallellkopplade. Sedan bestäms den totala laddningen av summan av alla laddningar som ackumuleras på plattorna på alla enheter. Och spänningsvärdet bestäms fortfarande enligt allmänna lagar. Därför är formeln för den totala kapacitansen för parallellkopplade kondensatorer:
С=(q 1 + q 2) / U.
Det vill säga att detta värde betraktas som summan av var och en av enheterna som används i anslutningen:
S=S 1 + S 2.
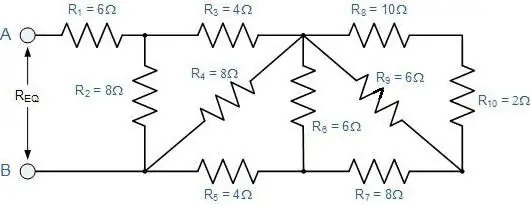
Hur bestämmer man det totala motståndet för en godtycklig anslutning av ledare?
Det vill säga en där på varandra följande avsnitt ersätter parallella och vice versa. För dem är alla beskrivna lagar fortfarande giltiga. Bara du behöver tillämpa dem i etapper.
Först är det tänkt att ment alt utöka systemet. Om det är svårt att föreställa sig det, måste du rita vad som händer. Förklaringen blir tydligare om vi överväger den med ett specifikt exempel (se figur).
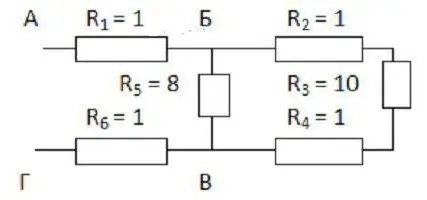
Det är bekvämt att börja rita från punkterna B och C. De måste placeras på ett visst avstånd från varandra och från arkets kanter. Till vänster närmar sig en tråd punkt B, och två är redan riktade till höger. Punkt B har å andra sidan två grenar till vänster och en tråd efter den.
Nu måste du fylla utrymmet mellan dessaprickar. Tre motstånd med koefficienterna 2, 3 och 4 ska placeras längs den övre ledningen, och den med index 5 kommer att gå från botten. De tre första är seriekopplade. Med det femte motståndet är de parallella.
De återstående två motstånden (det första och sjätte) är anslutna i serie med den aktuella sektionen av BV. Därför kan ritningen helt enkelt kompletteras med två rektanglar på vardera sidan om de valda punkterna. Det återstår att tillämpa formlerna för att beräkna motståndet:
- först den som ges för seriell anslutning;
- då för parallell;
- och igen i rad.
På detta sätt kan du distribuera vilket, till och med mycket komplext schema.
Problemet med seriekoppling av ledare
Skicka. Två lampor och ett motstånd är kopplade i en krets bakom varandra. Den totala spänningen är 110 V och strömmen är 12 A. Vad är värdet på motståndet om varje lampa är märkt till 40 V?
Beslut. Eftersom en seriekoppling övervägs är formlerna för dess lagar kända. Du behöver bara applicera dem korrekt. Börja med att ta reda på spänningsvärdet över motståndet. För att göra detta måste du subtrahera två gånger spänningen för en lampa från summan. Det visar sig 30 V.
Nu när två storheter är kända, U och I (den andra av dem anges i villkoret, eftersom den totala strömmen är lika med strömmen i varje serieförbrukare), kan vi beräkna motståndet för motståndet med hjälp av Ohms lag. Det visar sig vara 2,5 ohm.
Svar. Motståndets resistans är 2,5 ohm.
Uppgiftför anslutning av kondensatorer, parallella och serier
Skicka. Det finns tre kondensatorer med kapaciteter på 20, 25 och 30 mikrofarad. Bestäm deras totala kapacitans när de är anslutna i serie och parallellt.
Beslut. Det är lättare att börja med en parallellkoppling. I den här situationen behöver alla tre värdena bara läggas till. Den totala kapacitansen är alltså 75uF.
Beräkningarna blir något mer komplicerade när dessa kondensatorer är seriekopplade. När allt kommer omkring måste du först hitta förhållandet mellan enhet och var och en av dessa kapaciteter och sedan lägga till dem till varandra. Det visar sig att enheten dividerat med den totala kapaciteten är 37/300. Då är det önskade värdet cirka 8 mikrofarader.
Svar. Den totala kapacitansen i seriekoppling är 8 uF, parallellt - 75 uF.






