Som du vet tillhör varje fysisk storhet en av två typer, den är antingen skalär eller vektor. I den här artikeln kommer vi att överväga sådana kinematiska egenskaper som hastighet och acceleration, och även visa vart accelerations- och hastighetsvektorerna är riktade.
Vad är hastighet och acceleration?
Båda de kvantiteter som nämns i detta stycke är viktiga egenskaper för alla typer av rörelser, oavsett om det rör sig om att röra en kropp i en rak linje eller längs en krökt bana.
Speed är den hastighet med vilken koordinaterna ändras över tiden. Matematiskt är detta värde lika med tidsderivatan av tillryggalagd sträcka, det vill säga:
v¯=dl¯/dt.
Här är vektorn l¯ riktad från startpunkten för banan till slutpunkten.
Acceleration är i sin tur den hastighet med vilken själva hastigheten ändras över tiden. I form av en formel kan det skrivas så här:
a¯=dv¯/dt.
Självklart tar andraderivatan avförskjutningsvektor l¯ med tiden kommer vi också att få värdet på accelerationen.
Eftersom hastigheten mäts i meter per sekund, mäts accelerationen, enligt det skrivna uttrycket, i meter per sekund i kvadrat.

Var finns accelerations- och hastighetsvektorerna?
Inom fysiken kännetecknas varje mekanisk rörelse av en kropp vanligtvis av en viss bana. Det sistnämnda är någon imaginär kurva längs vilken kroppen rör sig i rymden. Till exempel är en rät linje eller en cirkel utmärkta exempel på vanliga rörelsebanor.
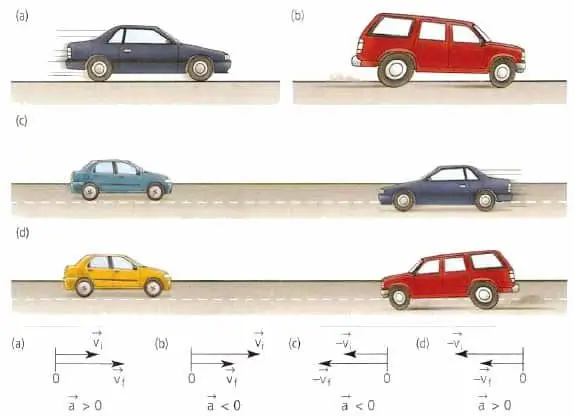
Kroppens hastighetsvektor är alltid riktad i rörelseriktningen, oavsett om kroppen saktar ner eller accelererar, om den rör sig i en rak linje eller längs en kurva. I geometriska termer riktas hastighetsvektorn tangentiellt till punkten för den bana i vilken kroppen för närvarande befinner sig.
Accelerationsvektorn för ett material eller en kroppspunkt har inget med hastighet att göra. Denna vektor är riktad i hastighetsändringens riktning. Till exempel, för rätlinjig rörelse kan värdet a¯ antingen sammanfalla i riktning med v¯ eller vara motsatt v¯.
Tvinga som verkar på kroppen och acceleration
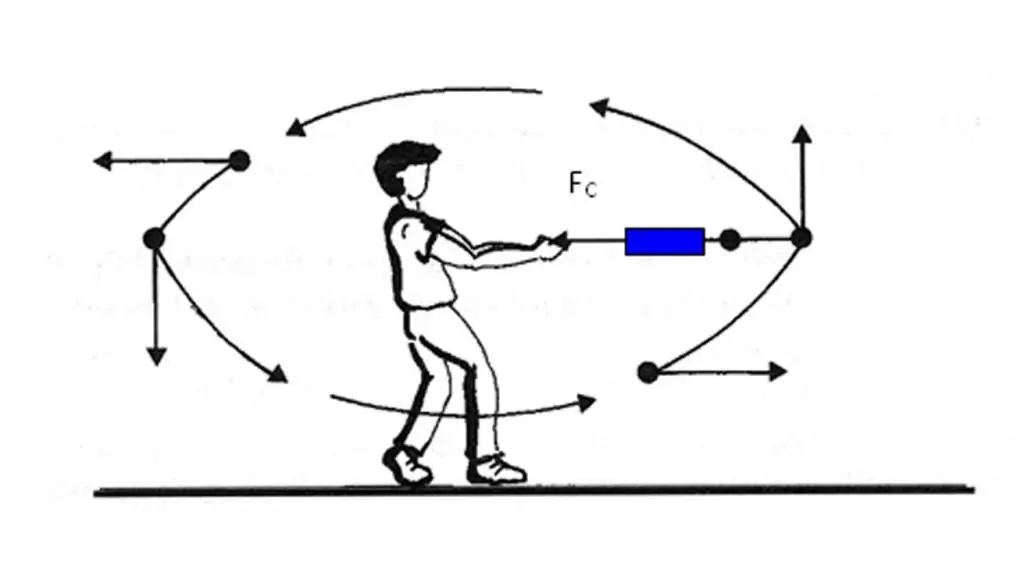
Vi har funnit att kroppens accelerationsvektor är riktad mot förändringen av hastighetsvektorn. Det är dock inte alltid lätt att avgöra hur hastigheten förändras vid en given punkt i banan. Dessutom, för att bestämma förändringen i hastighet, är det nödvändigt att utföra operationenvektorskillnader. För att undvika dessa svårigheter med att bestämma riktningen för vektorn a¯ finns det ett annat sätt att snabbt ta reda på det.
Nedan är Newtons berömda och välkända lag för varje student:
F¯=ma¯.
Formeln visar att orsaken till acceleration i kroppar är kraften som verkar på dem. Eftersom massan m är en skalär, är kraftvektorn F¯ och accelerationsvektorn a¯ i samma riktning. Detta faktum bör komma ihåg och tillämpas i praktiken närhelst det finns ett behov av att bestämma riktningen för kvantiteten a¯.
Om flera olika krafter verkar på kroppen, kommer accelerationsvektorns riktning att vara lika med den resulterande vektorn för alla krafter.
Cirkulär rörelse och acceleration
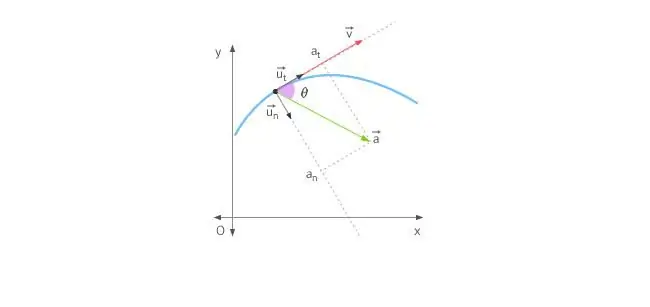
När en kropp rör sig i en rak linje, riktas accelerationen antingen framåt eller bakåt. Vid rörelse i en cirkel kompliceras situationen av att hastighetsvektorn hela tiden ändrar riktning. Mot bakgrund av ovanstående bestäms den totala accelerationen av dess två komponenter: tangentiella och normala accelerationer.
Tangentialacceleration riktas exakt likadant som hastighetsvektorn, eller mot den. Med andra ord är denna accelerationskomponent riktad längs tangenten till banan. Tangentiell acceleration beskriver förändringen i modulen för själva hastigheten.
Normal acceleration riktas längs normalen till den givna punkten i banan, med hänsyn till dess krökning. Vid cirkulär rörelse indikerar vektorn för denna komponenttill mitten, det vill säga den normala accelerationen riktas längs rotationsradien. Denna komponent kallas ofta centripetal.
Fullacceleration är summan av dessa komponenter, så dess vektor kan riktas godtyckligt med avseende på cirkellinjen.
Om kroppen roterar utan att ändra den linjära hastigheten, så finns det bara en normalkomponent som inte är noll, så fullaccelerationsvektorn riktas mot cirkelns centrum. Observera att detta centrum också påverkas av en kraft som håller kroppen på sin bana. Till exempel håller solens gravitationskraft vår jord och andra planeter i sina banor.






