Pyramid tillsammans med ett prisma är en perfekt polyeder i tredimensionellt utrymme, deras geometriska egenskaper studeras i gymnasiet. I den här artikeln kommer vi att överväga vad pyramiderna är, vilka element de består av och även kortfattat karakterisera de korrekta pyramiderna.
Geometrisk figurpyramid
Ur geometrisk synvinkel är pyramiden en rumslig figur som består av en polygon och flera trianglar. Att få denna siffra är ganska enkelt. För att göra detta, ta en polygon med n sidor, välj sedan en godtycklig punkt i rymden som inte kommer att ligga i polygonens plan, och anslut varje vertex av polygonen till denna punkt. Uppenbarligen kommer figuren som bildas på detta sätt att ha n trianglar kopplade till varandra vid en vertex.
För att visualisera den beskrivna figurens geometriska form, låt oss ta en bild.

Detta visar en fyrkantig pyramid, vars bas ärfyrhörning, och sidoytan är bildad av fyra trianglar som har en gemensam vertex.
Pyramidelement
Precis som vilken polyeder som helst, bildas pyramiden av tre typer av element:
- kanter;
- tops;
- ribs.
Ansikten är delar av plan som skiljer en figurs inre volym från det omgivande rummet. Om pyramidens bas innehåller en n-gon, är antalet ytor alltid n+1. Av dessa är n sidor triangulära och en sida är den nämnda n-gonala basen.
Vertices är punkter där tre eller flera ansikten på en figur skär varandra. Basområdet innehåller n hörn, som var och en är bildad av två triangulära ytor och en bas. Punkten där n triangulära sidor möts kallas toppen av pyramiden. Således består siffran i fråga av n+1 hörn.
Kanter är raka linjer som visas när två ansikten skär varandra. Varje kant begränsas av två hörn vid sina ändar. Varje pyramid med en n-gon bas innehåller 2n kanter. Hälften av detta tal, det vill säga n, bildas enbart av skärningspunkten mellan sidotrianglar.
Möjliga typer av figurer
Namnet på den aktuella figuren bestäms unikt av typen av polygon vid basen. Till exempel, om den har tre hörn och tre sidor, kommer pyramiden att vara triangulär, om fyra - fyrkantig, och så vidare.
Polygon kan vara konvex och konkav, såväl som vanlig och allmän typ. Allt detta avgör också pyramidens utseende.
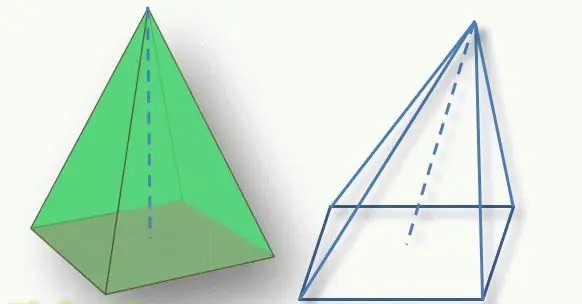
En viktig punkt för att bestämma typen av figur är läget för toppen av pyramiden i förhållande till dess bas. Det vinkelräta segmentet som dras från toppen till den polygonala basen kallas figurens höjd. Om detta segment skär basen i dess geometriska centrum (för en triangel är detta skärningspunkten mellan medianerna, för en fyrhörning skärningen av diagonaler), kallas figuren en rät linje. Annars talar de om en lutande pyramid.
Om basens n-gon är regelbunden (liksidig triangel, kvadrat, etc.), och figuren är rak, kallas den en vanlig pyramid.
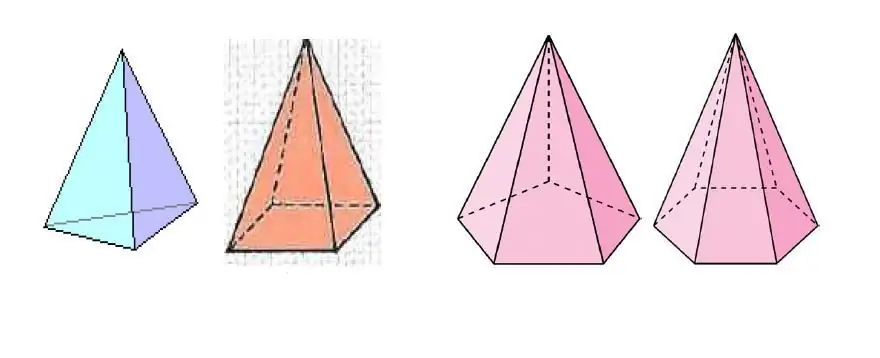
Bilden ovan visar flera pyramider, som skiljer sig åt i antalet sidor av polygonen vid basen.
Egenskaper för vanliga pyramider
Dessa pyramider skiljer sig från andra figurer i denna klass genom en hög grad av symmetri. I detta avseende är det bekvämt att utföra olika geometriska beräkningar med dem, till exempel volym eller ytarea.
En vanlig pyramid innehåller en n-gon vid sin bas, vars area bestäms unikt utifrån kunskapen om längden på dess sida. Figurens sidoyta är bildad av n identiska trianglar, som är liksidiga. Kanterna på en vanlig pyramid som ligger på sidoytan är lika med varandra. Värdet på längden på denna kant används ofta när man beräknar apotem för en figur och bestämmer ytan.
Höjden på en vanlig pyramid är den andra viktiga egenskapen hos figuren (den första är längden på kantengrunder). Höjd används vid beräkning av volym.
Vilket som helst plan parallellt med basen, som skär pyramidens sidoytor, leder till bildandet av en polygonal sektion. Det är homotetiskt med avseende på baspolygonen. Den beskrivna skivoperationen leder till bildandet av en hel klass av nya figurer - trunkerade vanliga pyramider.
De mest kända pyramiderna

Naturligtvis är dessa de vanliga fyrkantiga pyramiderna för de egyptiska faraonerna. På en plats som heter Giza finns det mer än 100 av dessa stenmonument, designens perfektion och noggrannheten hos de geometriska parametrarna som fortsätter att förvåna forskare till denna dag. Den största av dem är Keopspyramiden, som är cirka 146 meter hög och cirka 230 meter lång.
Vad exakt dessa pyramider tjänade till, samt med vilka mekanismer och när de byggdes, vet ingen än i dag.






