När man studerar fysik i årskurs 10, övervägs ämnet dipoler. Vad betyder detta begrepp och vilka formler används för att beräkna det?
Introduktion
Om du placerar en dipol i utrymmet för ett enhetligt elektriskt fält, kan du representera den som kraftlinjer. En dipol är ett system där det finns två laddningar som är identiska i parametrar, men de är motsatta punktladdningar. Dessutom kommer avståndet mellan dem att vara mycket mindre än avståndet till någon punkt i dipolfältet. Begreppet dipolmomentet studeras i skolkursen elektrodynamik (Åk 10).
Dipolens axel är en rät linje som går genom båda laddningarnas punkter. En dipolarm är en vektor som förbinder en laddning och som samtidigt går från negativt laddade partiklar till positivt laddade partiklar. En elektrisk dipol kännetecknas av närvaron av ett sådant tillstånd som en dipol eller elektriskt moment.
Per definition är ett dipolmoment en vektor som är numeriskt lika med produkten av dipolladdningen och dess arm. Dessutom är den samriktad med dipolens skuldra. Vid nolllikhet av summan av krafter, beräknar vi värdet av momentet. För vinkeln som finns mellan dipolmomentet ochdet elektriska fältets riktning, är närvaron av ett mekaniskt moment karakteristiskt.
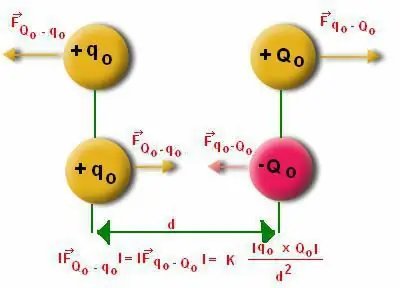
Ofta har människor svårt att beräkna modulen som verkar på dipolstrukturen. Här är det nödvändigt att ta hänsyn till särdragen med att beräkna vinkeln "Alfa". Det är känt att dipolen avviker från det balanserade läget. Men själva dipolmomentet har en återställande karaktär, eftersom det tenderar att vara i rörelse.
Beräkningar
När detta dipolmoment placeras i mediet av ett inhomogent elektriskt fält, uppstår oundvikligen en kraft. I en sådan miljö kommer indikatorerna för summan av krafter inte att vara noll. Följaktligen finns det krafter som verkar på dipolmomentet med en punktkaraktär. Storleken på dipolarmen är mycket mindre.
Formeln kan skrivas så här: F=q (E2 - E1)=qdE, där d är den elektriska fältskillnaden.
Sök efter egenskaperna hos det fysiska konceptet som studeras
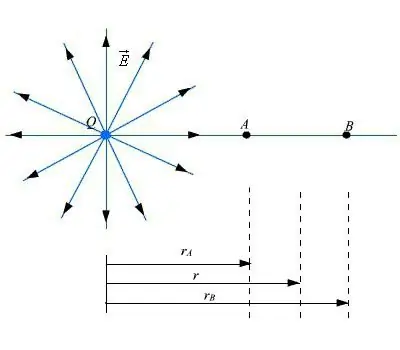
Låt oss titta närmare på ämnet. För att bestämma vad som är kännetecknet för det elektriska fältet, om det skapas med hjälp av ett system av laddningar och lokaliserat i ett litet utrymme, är det nödvändigt att göra ett antal beräkningar. Ett exempel presenteras av atomer och molekyler, som i sin sammansättning har elektriskt laddade kärnor och elektroner.
Om det är nödvändigt att söka efter ett fält på ett avstånd som är större än de dimensioner som utgör området där partiklarna finns, kommer vi att använda ett antal exakta formler som är mycket komplexa. Det går att använda enklareungefärliga uttryck. Låt oss anta att punktuppsättningar av laddningar qk deltar i skapandet av det elektriska fältet. De finns i ett litet utrymme.
För att utföra beräkningen av egenskapen som fältet har, är det tillåtet att kombinera alla laddningar i systemet. Ett sådant system betraktas som en punktladdning Q. Storleksindikatorerna kommer att vara summan av laddningarna som fanns i det ursprungliga systemet.
Debiteringsplats
Låt oss föreställa oss att platsen för laddningen anges på vilken plats som helst där avgiftssystemet qk finns. När du gör ändringar av platsen, om den har gränser uttryckta i ett litet område, kommer en sådan påverkan att vara försumbar, nästan omärklig för fältet vid synvinkeln. Inom sådana gränser för approximation av styrka och potential som det elektriska fältet har, görs bestämningar med traditionella formler.
När summan av systemets totala laddning är noll, kommer parametrarna för den angivna approximationen att se grova ut. Detta ger anledning att dra slutsatsen att det elektriska fältet helt enkelt saknas. Om det är nödvändigt att få en mer exakt uppskattning, samla ment alt in separata grupper av positiva och negativa laddningar av det system som övervägs.
I fallet med förskjutning av deras "centrum" i förhållande till andra, kan fältparametrarna i ett sådant system beskrivas som ett fält som har två punktladdningar, lika stora och motsatta i tecken. Det noteras att de är förskjutna i förhållande till andra. Att förseFör en mer exakt karakterisering av laddningssystemet i termer av parametrarna för denna approximation, kommer det att vara nödvändigt att studera egenskaperna hos en dipol i ett elektriskt fält.
Introduktion av termen
Låt oss gå tillbaka till definitionen. En elektrisk dipol är definitionen av ett system som har två punktladdningar. De har samma storlek och motsatta tecken. Dessutom är sådana skyltar placerade på små avstånd i förhållande till andra skyltar.
Du kan beräkna egenskapen för processen som skapas med hjälp av en dipol, och den representeras av två punktladdningar: +q och −q, och de är placerade på ett avstånd a i förhållande till de andra.

Beräkningssekvens
Låt oss börja med att beräkna potentialen och intensiteten som dipolen har på sin axiella yta. Detta är en rät linje som går mellan två laddningar. Förutsatt att punkt A är belägen på ett avstånd som är lika med r i förhållande till dipolens centrala del, och om den är r >> a, enligt principen om superposition för fältpotentialen vid denna punkt, kommer det att vara rationellt att använd uttrycket för att beräkna parametrarna för den elektriska dipolen.
Vektorns storlek beräknas genom superpositionsprincipen. För att beräkna fältstyrkan används begreppet förhållandet mellan potential och fältstyrka:
Ex=−Δφ /Δx.
Under sådana förhållanden indikeras riktningen för intensitetsvektorn longitudinellt i förhållande till dipolaxeln. För att beräkna dess modul är standardformeln tillämplig.
Viktigtförtydliganden
Det bör beaktas att försvagningen av det elektriska dipolfältet sker snabbare än det upplever en punktladdning. Avklingningen av dipolfältpotentialen är omvänt proportionell mot kvadraten på avståndet, och fältstyrkan är omvänt proportionell mot avståndets kub.
Med hjälp av liknande, men mer besvärliga metoder, hittas parametrarna för dipolens potential och fältstyrka vid godtyckliga punkter, vars positionsparametrar bestäms med hjälp av en sådan beräkningsmetod som polära koordinater: avståndet till mitten av den elektriska dipolen (r) och vinkeln (θ).
Beräkning med spänningsvektor
Begreppet intensitetsvektor E är uppdelat i två punkter:
- Radial (Er), som är riktad i längdriktningen relativt den raka linjen.
- En sådan rät linje förbinder den angivna punkten och mitten av dipolen med vinkelrät mot den Eθ.
Denna nedbrytning av varje komponent riktas längs förändringsförloppet som sker med alla koordinater för punkten som ska observeras. Du kan hitta det genom förhållandet som relaterar fältstyrkeindikatorer till potentiella ändringar.
För att hitta vektorkomponenten vid fältstyrkan är det viktigt att fastställa sambandets natur i de potentiella förändringar som uppstår på grund av förskjutningen av observationspunkten i vektorernas riktning.
Beräkna den vinkelräta komponenten
När det är klartFör denna procedur är det viktigt att ta hänsyn till att uttrycket för storleken vid en liten vinkelrät förskjutning kommer att bestämmas genom att ändra vinkeln: Δl=rΔθ. Storleksparametrarna för denna fältkomponent kommer att vara lika.
Efter att ha erhållit förhållandet är det möjligt att bestämma fältet för den elektriska dipolen vid en godtycklig punkt för att bygga en bild med kraftlinjerna för detta fält.
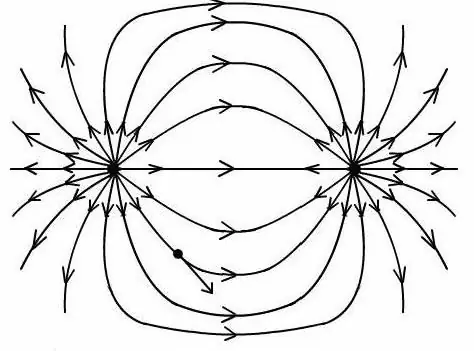
Det är viktigt att tänka på att alla formler för att bestämma potentialen och fältstyrkan för en dipol endast fungerar på produkten av de värden som en dipolladdning har och avståndet mellan dem.
Dipolmoment
Rubriken på det beskrivna arbetet är en fullständig beskrivning av den elektriska typen av egenskaper. Den har namnet "systemets dipolmoment".
Genom definition av en dipol, som är ett system av punktladdningar, kan man ta reda på att den kännetecknas av närvaron av axiell symmetri, när axeln är en rät linje som går genom flera laddningar.
För att ställa in hela karaktäristiken för dipolen, ange den orienteringsriktning som axeln har. För att förenkla beräkningarna kan dipolmomentvektorn specificeras. Värdet på dess storlek är lika med storleken på dipolmomentet, och riktningsvektorn skiljer sig genom sammanträffandet av den och dipolens axel. Så, p=qa om a är riktningen för vektorn som förbinder de negativa och positiva laddningarna av dipolen.
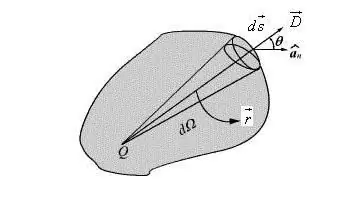
Användningen av en sådan egenskap hos dipolen är bekväm och gör det i de flesta fall möjligt att förenkla formeln och ge den formenvektor. Beskrivningen av potentialen för dipolfältet vid en punkt i en godtycklig riktning skrivs i form av en vektor.
Introduktionen av sådana begrepp som vektorkarakteristiken för en dipol och dess dipolmoment kan utföras med hjälp av en förenklad modell − en punktladdning i ett enhetligt fält, som inkluderar ett system av laddningar, vars geometriska dimensioner gör behöver inte tas med i beräkningen, men det är viktigt att känna till dipolmomentet. Detta är en förutsättning för att kunna utföra beräkningar.
Hur en dipol beter sig
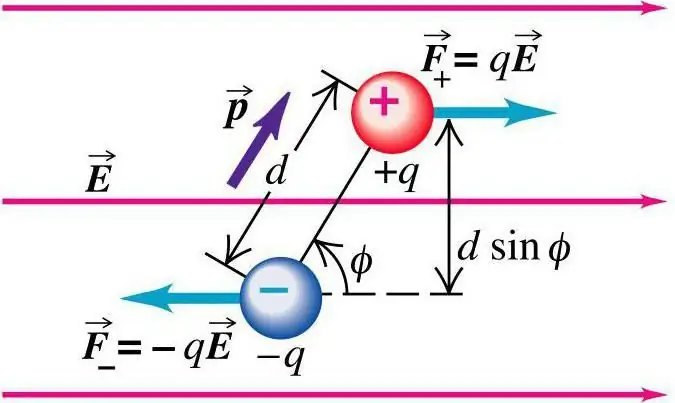
Beteendet hos en dipol kan ses på exemplet med en sådan situation. Positionen för två punktladdningar har en fast karaktär av avstånd i förhållande till varandra. De placerades i förhållande till en dipol med ett enhetligt elektriskt fält. Gjorde observationer om processen. I lektionerna i fysik (elektrodynamik) övervägs detta koncept i detalj. Från fältet till laddningen utförs krafternas verkan:
F=±qE
De är lika stora och motsatta i riktning. Indikatorn för den totala kraften som verkar på dipolen är noll. Eftersom en sådan kraft har en effekt på olika punkter blir det totala momentet:
M=Fa sin a=qEa sin a=pE sin a
med α är vinkeln som förbinder fältstyrkevektorerna och dipolmomentvektorerna. På grund av närvaron av ett kraftmoment tenderar systemets dipolmoment att återgå till riktningarna för den elektriska fältstyrkevektorn.
Elektrisk dipol är ett begrepp som är viktigt att förstå tydligt. Du kan läsa mer om det på Internet. Det kan det ocksåatt studera på fysiklektionerna i skolan i årskurs 10, som vi pratade om ovan.






